《物理化学》章末总结8

新的学期，新的物化。第八章介绍电解质。

第八章 电解质溶液

8.1 电化学中的基本概念和电解定律

能导电的物质称为导电体（electrical conductor），简称导体。导体可以分为电子导体和离子导体两类。

电子导体依靠自由电子的定向运动而导电，在导电过程中自身不发生化学变化。离子导体依靠离子的定向迁移导电。

接下来介绍原电池和电解池的概念。

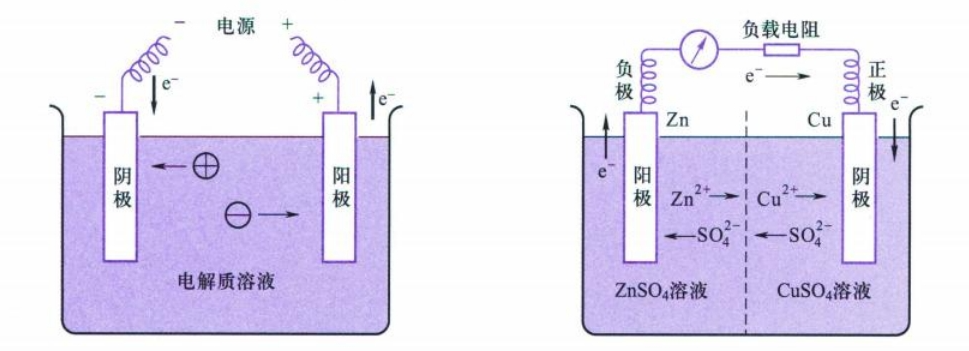
电化学中公认发生氧化作用的电极称为阳极，发生还原作用的电极称为阴极。物理学中会区分正负极的概念，此处需注意分辨，阴阳极和正负极在原电池和电解池中的对应关系不同。

在电极上发生的具体反应与电解质的种类、溶剂性质、电极材料、外加电压、离子浓度及温度有关，需具体分析。

Faraday归纳了多次试验结果，总结出Faraday电解定律（Faraday’s law of electrolysis）：

• 在电极上物质发生化学变化的物质的量与通入电荷量成正比。
• 若将几个电解池串联，通入一定电荷量后，在各个电解池的电极上发生化学变化的物质的量相等。

人们把$1mol$元电荷的电荷量称为Faraday常数，用$F$表示：

$$
F=Le=96484.5\ C\cdot mol^{-1}
$$

式中$L$为Avogadro常数，$e$是元电荷电荷量。

实际电解中，难免会发生副反应，因此得到一定量物质所需电荷量会比理论计算结果稍大，二者的比即定义为电流效率。

8.2 离子的电迁移率和迁移数

离子在外电场作用下发生的定向运动称为离子的电迁移（electromigration）。离子电迁移会使电极周围溶液浓度发生变化。

离子在电场中运动的速率除了与离子的本性及溶剂的性质有关以外，还与电场的电位梯度（electric potential gadient）$dE/dl$有关。显然电位梯度越大，离子运动的推动力也越大：

$$
r_+=u_+ \frac {dE}{dl} \quad r_-=u_- \frac {dE}{dl}
$$

式中的比例系数$u_+/u_-$称为离子电迁移率/离子淌度（ionic mobility）。

由于正负离子移动的速率不同、所带电荷不等，因此它们在迁移电荷量时所分担的份额也不同。把离子B所运载的电流与总电流之比称为离子B的迁移数（transference number），用$t_B$表示：

$$
t_B \xlongequal{def} \frac {I_B}{I}
$$

（ 迁移数是量纲为1的分数，用来衡量离子运载电流的能力，所以与离子移动速率以及下文的电导率联系起来都是很自然的。 ）

可以推导获得：

$$
t_+=\frac {I_+}{I}=\frac {r_+}{r_++r_-} \quad t_-=\frac {I_-}{I}=\frac {r_-}{r_++r_-}
$$

数学推导

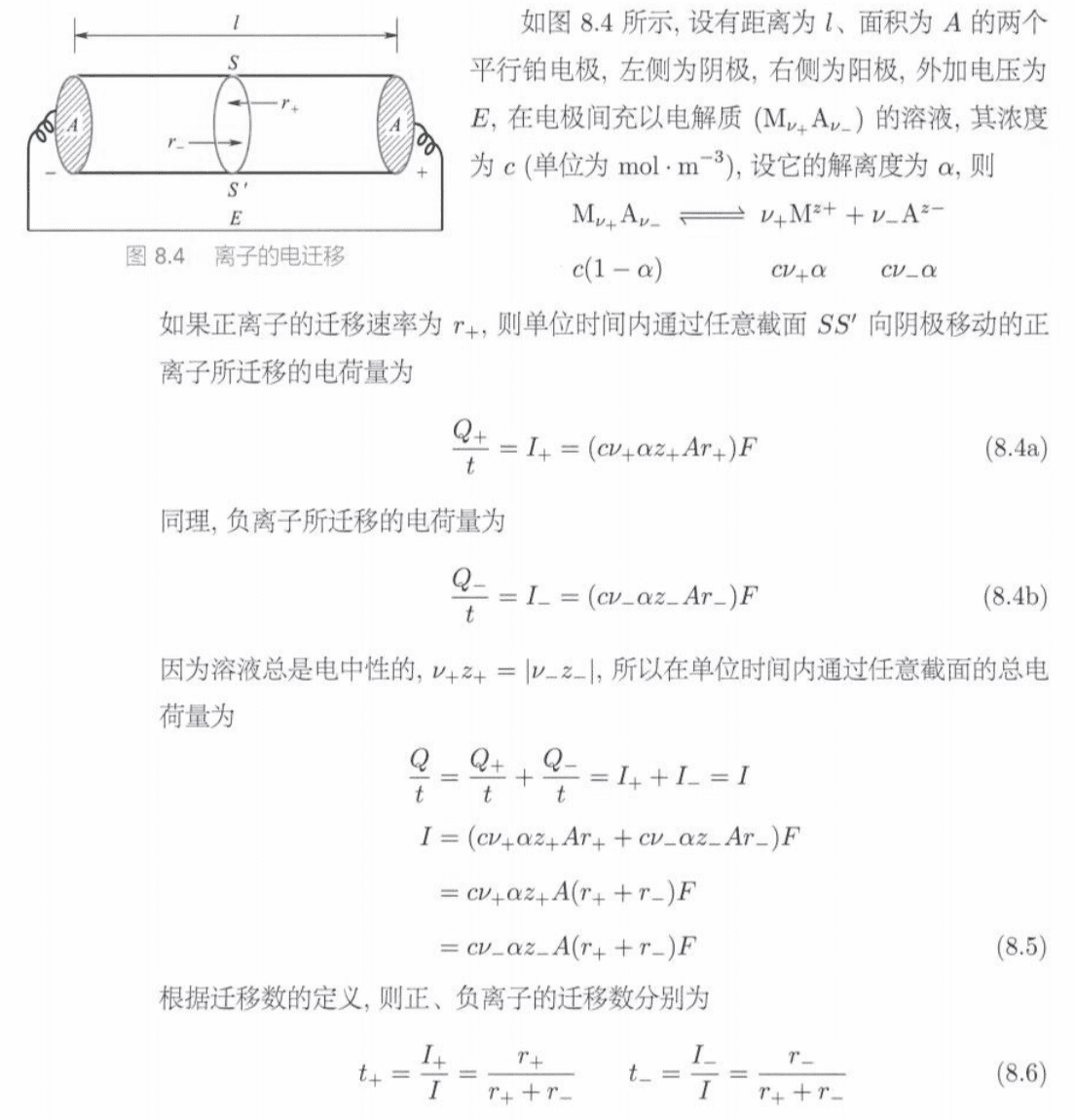
由于正负离子处于同一电位梯度中，因此：

$$
t_+=\frac {u_+}{u_++u_-} \quad t_-=\frac {u_-}{u_++u_-}
$$

若溶液中的正负离子不止一种，则任一离子B的迁移数为：

$$
t_B = \frac {Q_B}{Q} = \frac {I_B}{I} = \frac {n_Bz_Br_B}{\sum_B (n_Bz_Br_B)}
$$

测定离子迁移数的方法有Hittorf法、界面移动法和电动势法（见第九章）等。

具体的试验方法不在此详述。

8.3 电解质溶液的电导

物体的导电能力通常用电阻$R$表示。而对于电解质溶液，其导电能力则用电阻的倒数即电导（electric conductance）$G$来表示。

$$
G=\frac 1R
$$

导体的电阻与其长度$l$成正比，而与其截面积$A$成反比：

$$
R = \rho \frac lA
$$

式中$\rho$为电阻率（resistivity）。电导率（electric conductivity）$\kappa$是电阻率的倒数：

$$
\kappa = \frac 1{\rho}
$$

$$
G=\kappa \frac Al
$$

摩尔电导率（molar conductivity）$\Lambda_m$是指把含有$1mol$电解质的溶液置于间距为单位距离的电导池的两个平行电极之间时具有的电导。

$$
\Lambda_m \xlongequal {def} \kappa V_m = \frac {\kappa}{c}
$$

引入摩尔电导率的概念有利于对不同类型的电解质进行导电能力的比较。

测定电导的方式通常是先测出电阻，后计算电导。

$$
R=\rho \frac lA = \rho K_{cell}
$$

式中$K_{cell}$称为电导池常数（constant of a conductivity cell），因为一般情况下$l$和$A$很难测量，所以电导池需要用其他的已知电导的溶液测出电导池常数，再计算目标溶液的电导，购买的现成电导池通常会注明它的电导池常数。

强电解质溶液的电导率随浓度增大而升高，但当浓度增大到一定程度后，由于正负离子的相互作用力增大，离子运动速率降低，电导率反而降低。

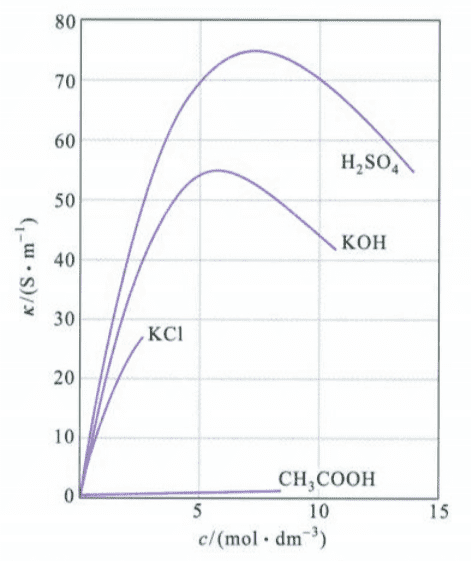
相对的，摩尔电导率随浓度的变化与电导率随浓度的变化不同。因为物质的量已经指定为$1mol$，当浓度降低时，离子之间相互作用力减弱，故摩尔电导率增大。

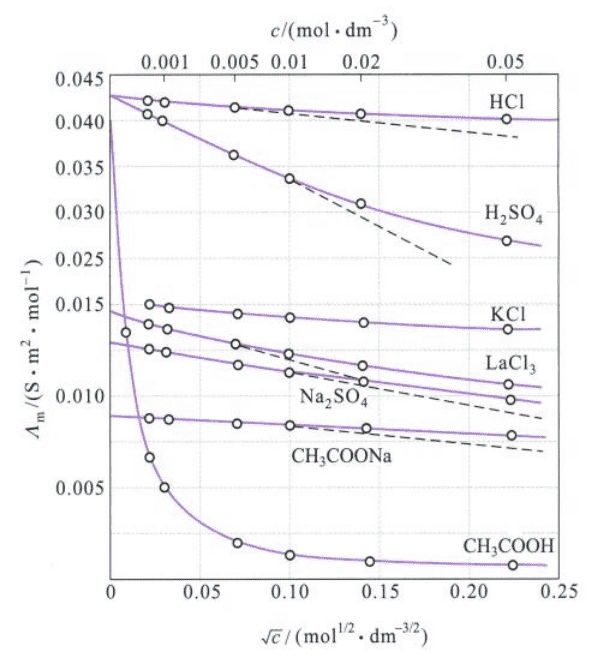
从图中可以发现，当浓度降低至一定程度后，摩尔电导率$\Lambda_m$和$\sqrt c$基本成线性关系：

$$
\Lambda_m = \Lambda_m^{\infin}(1-\beta \sqrt c)
$$

我们将直线外推至与纵坐标相交处，得溶液在无限稀释时的摩尔电导率$\Lambda_m^{\infin}$（limiting molar conductivity）。

（ 从表中还能发现，水溶液中的$H^+/HO^-$的离子摩尔电导率非常大，这种异常现象只在水溶液或含羟基的溶剂中显现。有人认为水溶液中质子的传导通过Grotthus电导机理完成，即质子携带电流沿着氢键被传导。 ）

强电解质的$\Lambda_m^{\infin}$可用外推法推出，但是弱电解质的摩尔电导率受浓度影响很大，很难从试验中直接求得，我们下面介绍Kohlrausch的离子独立移动定律以解决这个问题。

Kohlrausch根据大量的试验数据发现了一个规律，即在无限稀释的溶液中，每一种离子都是独立移动的，不受其他离子的影响。

这意味着每一种离子对$\Lambda_m^{\infin}$值都有恒定的贡献，因而电解质的$\Lambda_m^{\infin}$可认为是两种离子的极限摩尔电导率之和，这就是离子独立移动定律（law of independent migration）。

$$
\Lambda_m^{\infin} = \Lambda_{m,+}^{\infin} + \Lambda_{m,-}^{\infin}
$$

更一般的，对于电解质$M_{v_+}A_{v_-}$，其一般的表达式为：

$$
\Lambda_m^{\infin} = v_+\Lambda_{m,+}^{\infin} + v_-\Lambda_{m,-}^{\infin}
$$

据此，弱电解质的$\Lambda_m^{\infin}$就可以从强电解质的$\Lambda_m^{\infin}$求算，例如：

$$
\begin{aligned} \Lambda_m^{\infin}(HAc) &= \Lambda_m^{\infin}(H^+) + \Lambda_m^{\infin}(Ac^-) \[3mm]
&= [\Lambda_m^{\infin}(H^+) + \Lambda_m^{\infin}(Cl^-)] + [\Lambda_m^{\infin}(Na^+) + \Lambda_m^{\infin}(Ac^-)]-[\Lambda_m^{\infin}(Na^+) + \Lambda_m^{\infin}(Cl^-)] \[3mm]
&= \Lambda_m^{\infin}(HCl) + \Lambda_m^{\infin}(NaAc) - \Lambda_m^{\infin}(NaCl) \end{aligned}
$$

电解质的摩尔电导率是正负离子的离子摩尔电导率贡献的总和，所以离子的迁移数也可以看作某种离子的离子摩尔电导率占电解质的摩尔电导率的分数。

（ 这一推论总体上还是很符合直觉的。 ）

$$
t_+ = \frac {\Lambda_{m,+}^{\infin}}{\Lambda_m^{\infin}} \quad t_- = \frac {\Lambda_{m,-}^{\infin}}{\Lambda_m^{\infin}}
$$

离子的摩尔电导率可以由离子的电迁移率求得，进而可以推出其与离子淌度的关系：

$$
\Lambda_{m,+} = z_+u_+F \quad \Lambda_{m,-} = z_-u_-F
$$

下面简述电导测定的一些应用：

• 检验水的纯度：通过检验水的电导，就可知其纯度是否符合要求。工业上要求的“电导水”的电导率需在$1 \times 10^{-4}\ S\cdot m^{-1}$以下。
• 计算弱电解质的解离度和解离常数：弱电解质并非完全解离，只有解离的部分才能传递电流。因此由于弱电解质的不完全解离，一定浓度下的$\Lambda_m$称为表观摩尔电导率，并且满足$\Lambda_m/\Lambda_m^{\infin}=\alpha$，其中$\alpha$为解离度。有了解离度，那么解离常数也就不难获得了。
• 测定难溶盐的溶解度：在获得饱和溶液的电导率之后，再测定溶液摩尔电导率，就可以求出难溶盐的溶解度。注意由于难溶盐的溶液极稀，不能忽略水的电导率，必须减去。
• 电导滴定：利用溶液电导的变化来确定滴定终点。

8.4 电解质的平均活度和平均活度因子

在电解质溶液中，正负离子同时存在且互相吸引，所以其相互作用往往会使得溶液无法看作理想溶液。

非理想溶液不遵从化学势的公式，为了让热力学计算仍能保持简单的数学关系，Lewis提出了活度的概念：

$$
\alpha_{m,B} = \gamma_{m,B} \frac {m_B}{m^{\ominus}}
$$

引入活度修正后，化学势的表示为：

$$
\mu_B = \mu_B^{\ominus}(T) + RT\ln \alpha_{m,B}
$$

对于电解质溶液，电解质解离为正负离子，对于各种正负离子，分别有：

$$
\alpha_+ = \gamma_+ \frac {m_+}{m^{\ominus}} \quad \alpha_- = \gamma_- \frac {m_-}{m^{\ominus}}
$$

式中$\alpha_+/\alpha_-$表示正/负离子的活度，$m_+/m_-$表示正/负离子的质量摩尔浓度。

在电解质溶液中，正负离子总是同时存在的，但我们还没有严格的试验方法可以用来测定单个离子的活度和活度因子，于是我们提出离子平均活度因子的概念以便通过试验方法测定（以$HCl$为例）：

$$
a_{\pm} \xlongequal {def} (a_{H^+}a_{Cl^-})^{1/2} \[3mm]
m_{\pm} \xlongequal {def} (m_{H^+}m_{Cl^-})^{1/2} \[3mm]
\gamma_{\pm} \xlongequal {def} (\gamma_{H^+}\gamma_{Cl^-})^{1/2}
$$

上述物理量分别为正负离子的平均活度（mean activity of ions），平均质量摩尔浓度（mean molality of ions）和平均活度因子（mean activity factor of ions）。

对于任意强电解质$M_{v_+}A_{v_-}$，则有：

$$
a_{\pm} \xlongequal {def} (a_{+}^{v_+}a_{-}^{v_-})^{1/v} \[3mm]
m_{\pm} \xlongequal {def} (m_{+}^{v_+}m_{-}^{v_-})^{1/v} \[3mm]
\gamma_{\pm} \xlongequal {def} (\gamma_{+}^{v_+}\gamma_{-}^{v_-})^{1/v}
$$

式中$v=v_+ + v_-$。

如果查询活度因子的数据，我们会发现，在稀溶液中，影响离子平均活度因子$\gamma_{\pm}$的主要因素是离子的浓度和价数，且离子价数的影响比浓度影响更大。

综合这些信息，在1921年，Lewis和Randall提出了离子强度（ionic strength）的概念：

$$
I \xlongequal {def} \frac 12 \sum_B m_Bz_B^2
$$

Lewis根据试验进一步指出：离子平均活度因子和离子强度的关系在稀溶液的范围内符合如下的经验式：

$$
\lg \gamma_{\pm} = -C\sqrt I
$$

离子强度的概念最初是从实验数据中归纳总结出的，但是在下文Debye-Hückel理论所导出的关系式中，很自然地出现了与离子强度有关的一项，并且与经验关系是一致的。

8.5 强电解质溶液理论简介

在人们研究电解质溶液的依数性时，发现电解质溶液的依数性比相同浓度的非电解质溶液依数性数值大得多。历史上van’t Hoff曾经用系数$i$来表示这种偏差：

$$
i= \frac {\Pi_{实验}}{\Pi_{计算}}
$$

后来，Arrhenius提出了部分解离学说，用解离度的概念解释这种现象，但是此学说用于强电解质则会得到相互矛盾或者与实验值不符的结果。

在经典的电离学说中，没有考虑离子之间的相互作用，对于弱电解质溶液，由于离子浓度不大，所以忽略离子间的相互吸引作用也无所谓。但是对于强电解质，离子之间的相互静电吸引力就不能忽略。

Debye和Hückel于1923年提出了强电解质溶液的理论，也称为离子互吸理论（interionic attraction theory）。

Debye和Hückel提出了离子氛（ionic atmosphere）的概念，即认为溶液中每一个离子都被电荷符号相反的离子所包围，由于离子的相互作用使得离子的分布不均匀，从而形成了离子氛。离子氛的电荷在数值上要等于中心离子的电荷，只是符号相反。

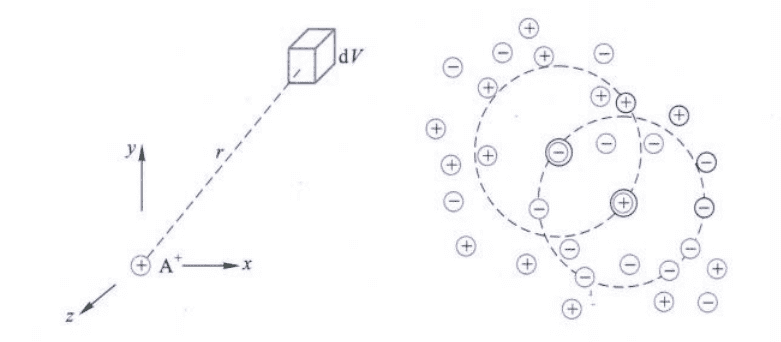
离子氛的构成错综复杂，且离子氛不是完全静止的，而是在不断运动和变换，所以离子氛的存在只能看作时间统计的平均结果。

基于离子氛概念和其余几个基本假定，Debye和Hückel给出了稀溶液中离子活度因子的计算公式：

$$
\lg \gamma_i = -Az_i^2 \sqrt I
$$

上式为Debye-Hückel极限定律（Debye-Hückel’s limiting law），之所以称为极限定律，是因为在推导过程中的一些假设只有在溶液非常稀释时才会成立。

根据这个公式可以推出，$\lg \gamma_i$与$\sqrt I$成线性关系，在低浓度情况下与试验结果相符。

1927年，美国物理化学家Onsager将Debye-Hückel理论应用到有外加电场作用的电解质溶液，从而形成了Debye-Hückel-Onsager电导理论。

在外加电场下，离子氛对离子运动的影响产生于下列两个原因：

• 弛豫效应（relaxation effect）：在外加电场下，离子的运动会破坏离子氛，同时离子氛也在重建，从破坏到重建的过程需要时间，称为弛豫时间，同时由于离子一直在运动，所以离子氛在没完全破坏也没完全生成的状态，就会出现不对称的离子氛，会阻碍中心离子的运动，称为弛豫力。
• 电泳效应（electrophoresis effect）：电场使得中心离子移动，同时让它的离子氛向反方向移动，离子移动时携带的溶剂化分子互相阻碍，增加了粘滞力，阻碍了离子的移动。

从Debye-Hückel-Onsager电导理论出发能推出：

$$
\Lambda_m = \Lambda_m^{\infin} - A\sqrt c
$$

这与先前Kohlrausch的经验公式一致。

（ Debye-Hückel理论虽然能用于稀溶液，但是理论仍然存在缺陷。这个理论完全忽略了离子的溶剂化作用，同时忽略了离子自身的性质、结构和溶剂化能力。 ）

总结

本章是电解质溶液的介绍，相对无机化学内容来说更细致，不过模型是不太复杂的。