《物理化学》章末总结9

第九章讲原电池。

第九章 可逆电池的电动势及其应用

9.1 可逆电池和可逆电极

将化学反应转变为一个能够产生电能的装置，首要条件是该化学反应是一个氧化还原反应，或者在反应过程中经历了氧化还原的过程。其次必须给予适当的装置，使得化学反应分别在电极上完成。

电池根据电解质溶液的设置可以分为单液电池和双液电池，即把电极插入同一种电解质溶液还是两种不同的电解质溶液。双液电池有时会使用盐桥相连，以便减小液接电势。

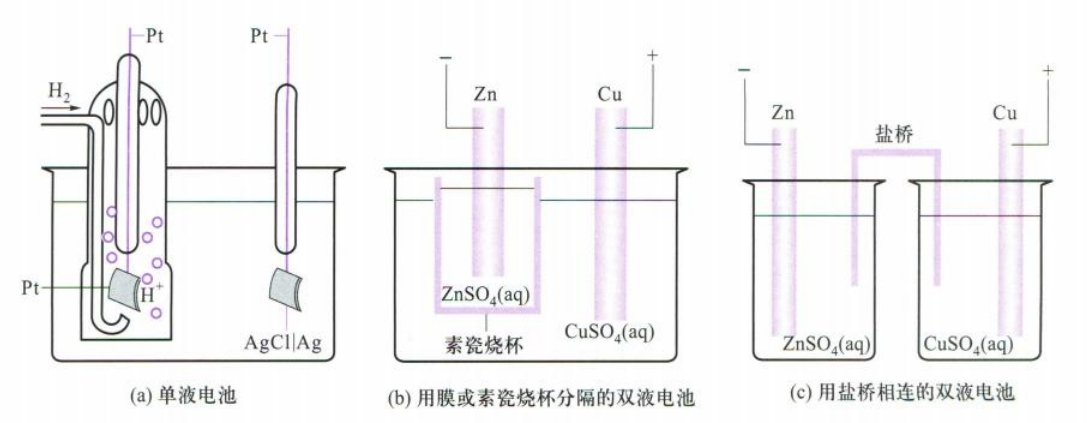
我们本章讨论的电池均为可逆电池（reversible cell），因为只有可逆电池电动势才能与热力学相联系。

要构成可逆电池，电极反应必须是可逆的，更具体的有以下两个条件：

• 电极上的反应可向正、反两个方向进行。电池上的化学反应可以逆向进行，化学反应满足可逆性。
• 可逆电池在工作时通过的电流必须十分微小，即电池是在接近平衡状态的情况下工作的。类似于热力学中的准静态过程，这一点说明能量转移的可逆性。

构成可逆电池的电极必须是可逆电极，有以下三种类型：

• 第一类电极：金属浸入含该金属离子的溶液中，例如$Zn(s)|ZnSO_4(aq)$。同属一类电极的还有氢电极、氧电极、卤素电极和汞齐电极等。
• 第二类电极：金属及其表面覆盖一层该金属的难溶盐，然后浸入含该难溶盐的负离子的溶液，如$Cl^-(\alpha_-)|AgCl(s)|Ag(s)$。同属二类电极的还有难溶氧化物电极。
• 第三类电极：惰性金属插入某种离子不同氧化态的溶液，又称氧化还原电极，如$Fe^{3+}(\alpha_1),Fe^{2+}(\alpha_2)|Pt(s)$。

9.2 电动势的测定

电池电动势不能直接用伏特计来测量，因为要想让伏特计显示示数必须有适量的电流通过，这样就不满足可逆电池微小电流的条件。

所以测量电池电动势时我们需要另辟蹊径，Poggendorff对消法是一个可行方案。我们在外电路上加一个方向相反而电动势几乎相等的电池，以对抗原电池的电动势，相当于电路中有一个无限大的电阻，因此电流十分微小，可以看作满足可逆电池的条件。

按照上述方案，我们需要一个电动势已知且稳定不变的辅助电池，此电池称为标准电池。常用的标准电池是Westom电池。

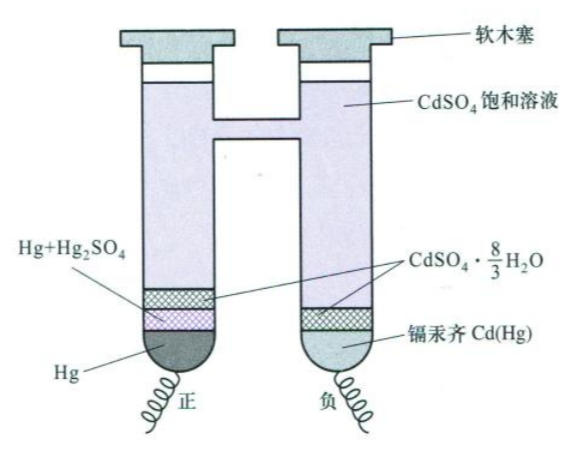
Weston标准电池电动势只与镉汞齐的活度有关，而用于制备标准电池的镉汞齐的活度在一定温度下有定值，所以标准电池电动势可以由与温度相关的经验公式直接求得。

9.3 可逆电池的书写方法及电动势的取号

可逆电池有一套约定俗成的惯例如下：

• 写在左边的电极起氧化作用，为负极；写在右边的电极起还原作用，为正极。
• 用“|”表示相界面，有界面电势存在。
• 用“||”表示盐桥，说明液接电势通过盐桥以降低到可忽略不计。
• 注明温度、压力、物质物态、物种活度等。
• 电池电动势等于右边电极的还原电极电势减去左边负极的还原电极电势。

书写电池和电池反应的内容已经是老生常谈，在此不多叙述。

我们知道电动势$E$与热力学量$\Delta_rG_m$相联系（$\Delta_rG_m = -zFE$），所以$E$的取号与$\Delta_rG_m$相反，这就说明当电池反应能够自发时，$E>0$，反之同理。

9.4 可逆电池的热力学

根据化学反应等温式以及电动势与吉布斯自由能变的关系，可以推导出Nerst方程，对于一般反应：

$$
cC+dC = gG+hH
$$

则其Nerst方程为：

$$
E=E^{\ominus}-\frac {RT}{zF}\ln \frac {a_G^g a_H^h}{a_C^c a_D^g} = E^{\ominus}-\frac {RT}{zF} \ln \prod_B a_B^{v_B}
$$

数学推导

图中式（9.2b）为：$(\Delta_rG_m)_{T,p}=\frac {-nEF}{\xi} = -zEF$

上式称为电池反应的Nerst方程，它将电池的电动势与其标准电动势和各组分活度联系起来。

若电池反应中各参加反应的物质都处于标准状态，则：

$$
\Delta_rG_m^{\ominus} = -zE^{\ominus}F = -RT \ln K_a^{\ominus}
$$

因此：

$$
E^{\ominus} = \frac {RT}{zF} \ln K_a^{\ominus}
$$

这给了我们一个通过标准电动势求得反应标准平衡常数的方法，电池的标准电动势又可以通过标准电极电势计算得到。

根据热力学公式，我们能够进一步求得其他热力学量：

$$
\Delta_rS_m = zF \left(\frac {\partial E}{\partial T} \right)_p \[3mm]
\Delta_rH_m = \Delta_rG_m+T\Delta_rS_m = -zEF+zFT \left(\frac {\partial E}{\partial T} \right)_p
$$

数学推导

9.5 电动势产生的机理

一个电池的总的电动势可能由下列几种电势差所构成，即电极与电解质溶液界面间的电势差、导线与电极之间的接触电势差以及由于不同的电解质溶液之间或同一电解质溶液但浓度不同而产生的液体接界电势差。

接下来依次讨论这三种电势差。

如果把一种金属片插入水中，水分子会水合金属离子，使得一部分金属离子进入溶液中，因此金属表面显示负电荷，溶液因有金属离子进入而显正电荷。

这种因金属和溶液之间由于电荷不均所产生的电势差称为表面电势，常用双电层（electrical double layer）模型来描述，溶液中的金属离子受电极相反电荷的吸引而聚集在电极表面周围的溶液中，这一层溶液称为紧密层（compact layer），也有一些离子因热运动远离金属表面，扩散到溶液其他部分，称为扩散层（diffuse layer）。

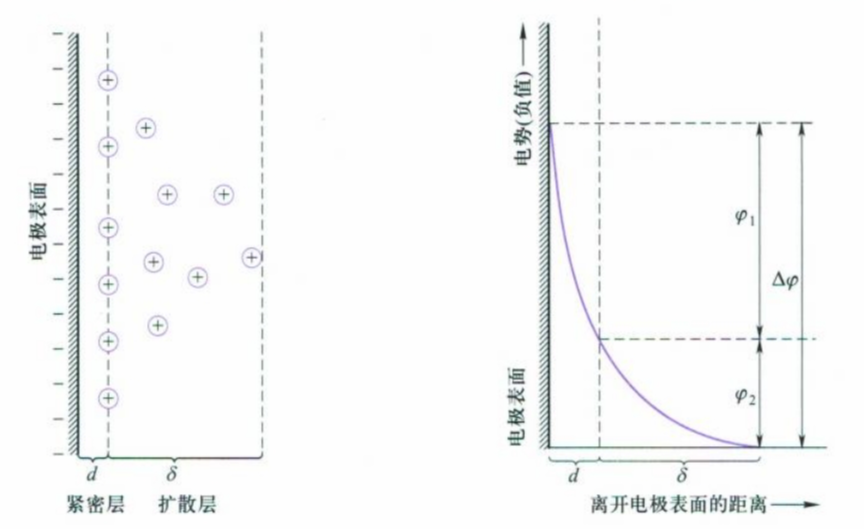
当两种金属相接触时，在界面上产生的电势差称为接触电势（contact potential）。电池中导线和电极相互连接时必然会产生接触电势，这也是构成整个电池电动势的一部分。

在两种含不同溶质的溶液所形成的界面上，或两种溶质相同而浓度不同的溶液界面上存在的电势差称为液体接界电势（或液接电势，liquid junction potential）。由于离子迁移速率的不同，从而溶液中带有不同电荷的离子分布不均，进而产生了液接电势。

液接电势可以通过考虑离子迁移而计算得到，此处仅给出结果。

对于1-1价型电解质溶液：

$$
E_j = (t_+ - t_-)\frac {RT}{F} \ln \frac {m}{m’} = (2t_+ - 1)\frac {RT}{F}\ln \frac {m}{m’}
$$

对于高价型电解质溶液$[M^{z+}A^{z-}(m_1)|M^{z+}A^{z-}(m_2)]$：

$$
E_j = \frac {\frac {\Lambda_{m,+}}{z_+} - \frac {\Lambda_{m,-}}{z_-}}{\Lambda_{m,+}+\Lambda_{m,-}} \frac {RT}{F} \ln \frac {m_1}{m_2}
$$

两种金属插入溶液中后，金属离子进入溶液同时金属又沉积回电极，达到平衡后建立稳定的电势差。但是两种金属的电势不等，如果用导线连接，电势更小的电极会给出电子，这会破坏两个电极的双电层，因此氧化还原反应开始自发进行，这就是原电池的电动势的产生。

9.6 电极电势和电池的电动势

原电池是由两个相对独立的电极组成的，每个电极相当于一个“半电池”（half cell），分别进行氧化和还原作用。

但是我们不能测定或计算单个电极的电极电势，而只能测得由两个电极所组成的电池的总电动势。因此我们可以选定一个电极作为标准，这样就可以获得其他电极相对标准电极的电极电势。

按照IUPAC的建议，采用标准氢电极作为标准电极，按照这个规定，电极的氢标电极电势就是所给电极于同温下的标准氢电极所组成的电池的电动势。

把镀铂黑的铂片插入含氢离子的溶液中，并不断将氢气冲打到铂片上，若氢气分压为$p^{\ominus}$，且氢离子活度等于1，则为标准氢电极。

标准氢电极的电极电势规定为0，所以与标准氢电极组合为原电池的电极的电极电势就是电池电动势（标准氢电极作负极）。通过这种方法，我们就可以把各种电极的电极电势都求得并排序制成表格，称为电动序（electromotive series）。

利用电动序可以估计电解过程中溶液离子在电极上发生还原反应的先后次序，以及判断氧化还原反应自发进行的方向。电极电势越负，则电对的还原态还原性越强；电极电势越正，则电对的氧化态氧化性越强。

同样的，可以推导出电极的Nerst方程：

$$
\varphi_{Ox|Red} = \varphi_{Ox|Red}^{\ominus} - \frac {RT}{zF} \ln \frac {a_{Red}}{a_{Ox}}
$$

在实际使用时，氢标电极的使用条件十分严苛，制备和纯化都较复杂，所以往往采用二级标准电池，如甘汞电极（calomel elctrode）等。它的电极电势可以被精准测定，在一定温度下电极电势稳定，且易于制备，使用方便。

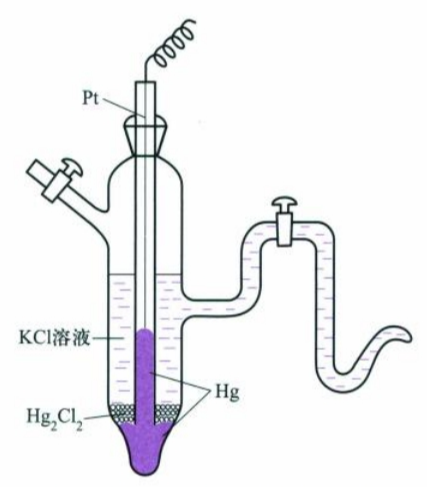
有了电极电势，可以计算出电池电动势，即$E=\varphi_{Ox|Red}(右)-\varphi_{Ox|Red}(左)$。注意使用电极电势时需要注意电极反应的电子数需要保持一致。

或者可以从电池的总反应式直接用Nerst方程计算电池电动势，此法与电极电势法实际上是相同的。

9.7 电动势测定的应用

利用电动势可以求得电池反应的各种热力学量、判断氧化还原反应进行方向等，本节介绍几种其他的应用：

• 求电解质溶液的平均活度因子。利用Nerst方程的关系，已知电池电动势和电池标准电动势就可以求得电解质$\gamma_{\pm}$值。
• 求难溶盐的活度积$K_{sp}$。可以设计一个合适的电池，使得电池的净反应恰为难溶盐的溶解反应，那么只要得到该电池的电动势就自然得到反应的平衡常数，也即活度积。类似的，还可以用相同方法获得弱酸/碱的解离常数。
• $pH$的测定。测定$pH$常用玻璃电极，它是一种氢离子选择性电极（selective electrode），用玻璃电极与另一甘汞电极组成电池，就能从测得的$E$值求出溶液的$pH$。
  （ 玻璃电极内部包括一个内参比电极（通常是$Ag|AgCl$电极）和确定浓度的盐酸溶液，提供一个稳定浓度的$H^+$体系。内参比电极和另一个电极（常为甘汞电极）组成电池，并且具有确定的电动势（只与$Cl^-$活度有关），而玻璃电极的玻璃膜会在内、外溶液产生氢离子浓度差，因此产生液接电势。附加的液接电势只与外部溶液的氢离子浓度有关，具有函数关系，因此测得电动势就能得到外部溶液$pH$。 ）
• 电势-$pH$图。把一些含$H^+/OH^-$参加的电极电势与$pH$的有关绘制成图，就可以从图上直接判断，在一定的$pH$范围内何种电极反应会优先进行，这种图就称为电势-$pH$图，或称Pourbaix图。

9.8 内电位、外电位和电化学势

本节内容超出了课程介绍的范围，仅作简要说明。

物理学中，某一位置的电位$\varphi$是指把单位正电荷从无穷远处移到该处所做的电功，但是在化学体系里，带电荷物种进入物相时必然伴随化学反应，所以无法只简单地考虑电学部分而忽略化学部分。

物体内一点的内电位$\varphi$（inner potential）即为物理意义中的电位，但是实际上无法测出内电位，不得不把内电位分为两部分，外电位$\psi$（outer potential）和表面电势$\chi$（surface potential）。

外电位指把单位正电荷从真空无穷远处移到物体表面的近旁所做的电功（约距物体表面$10^{-4}cm$左右）。表面电势即为把单位电荷从表面附近通过界面移到物相内部的电功。即：

$$
\varphi = \psi + \chi
$$

把实验电荷移入物相中时，除了要克服表面电势外，还要克服粒子之间的短程作用的化学功，这个功就是化学势$\mu$。

那么上述过程要做的总功为：

$$
W = ze\psi + ze\chi + \mu = ze\varphi + \mu = \overline \mu
$$

$\overline \mu$为实验电荷在物相内的电化学势（electrochemical potential）。

总结

这一章写得挺慢。