《物理化学》章末总结11

第十一章为化学动力学，分为上下两部分，上部分基本是无机化学里学过的知识点。

第十一章 化学动力学基础（一）

11.1 化学动力学的任务和目的

化学动力学的任务包括研究反应进行的速率和研究反应历程。前者告诉我们什么因素能够影响反应速率，可以让我们更具需要调整反应的速率；后者告诉我们反应物究竟是通过什么步骤转化为最终产物，有助于让我们了解物质运动形态的知识。

11.2 化学反应速率的表示法

化学反应的速率可以通过反应物或生成物浓度随时间的变化来表示，如果我们把反应过程中各物质的浓度与时间的关系绘制成曲线，那么曲线斜率就可以很好的表示反应速率：

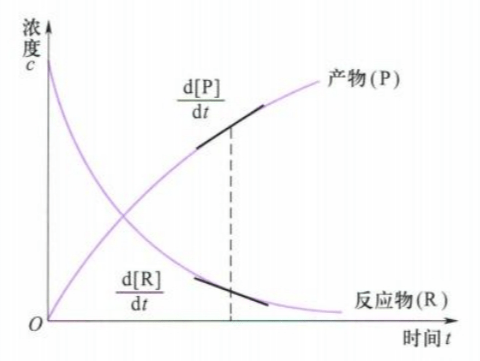
对于给定反应，不难写出其反应进度$\xi$：

$$
\begin{aligned} &\alpha R\quad \longrightarrow &&\beta P \[3mm] t=0 \quad&n_R(0) &&n_P(0) \[3mm] t=t \quad &n_R(t) &&n_P(t) \end{aligned}
$$

$$
\xi = \frac {n_R(t)-n_P(0)}{-\alpha} = \frac {n_P(t)-n_P(0)}{\beta}
$$

将反应进度对$t$微分，即获得反应的转化速率（conversion rate of reaction）：

$$
\frac {d\xi}{dt} = \dot \xi = -\frac 1{\alpha}\frac {dn_R(t)}{dt} = \frac 1{\beta} \frac {dn_P(t)}{dt}
$$

由于很多时候反应都在恒容容器中发生，所以可从反应的转化速率推得反应速率：

$$
r \overset{def}{=} \frac {1}{V}\dot \xi = -\frac 1{\alpha}\frac {d[R]}{dt} = \frac {1}{\beta}\frac {d[P]}{dt}
$$

负号的存在是为了让反应速率始终保持正值。

除了使用浓度表示，对于气相反应，也可以用各物质的分压表示；对于多相催化反应，通常还考虑催化剂的影响，例如：

$$
r_A = \frac 1A \frac {d\xi}{dt}
$$

上式中$r_A$称为表面反应速率（areal rate of reaction），表示的是单位表面积催化剂的反应速率，$A$为催化剂的表面积。

不难看出，使用反应进度/反应速率的好处在于可以统一表示整个反应的反应情况，而不会受到反应式的化学计量比的影响。

测定反应物或产物在不同反应时间的浓度一般可采用化学方法或物理方法。化学方法是在某一时间取出一部分物质，令反应迅速停止，然后进行化学分析；物理方法是监测与浓度有关的物理量的变化来实现原位测定。

11.3 化学反应的速率方程

表示反应速率与浓度等参数之间的关系的方程称为反应的速率方程（rate equation），或称动力学方程，速率方程可表示为微分式或积分式。

在讨论速率方程前，有必要先介绍基元反应（elementary reaction）的概念。

一个化学反应往往并不像化学方程式所写的那样反应，而是经过若干个最简单、最基础的反应步骤才最终形成产物分子，这些简单的反应需要满足：分子经一次碰撞后，在一次化学行为中就能完成反应，这样的反应就是基元反应。

通常一个一般反应包含若干步基元反应，这些基元反应就代表了反应所经的途径和历程，在动力学上称其为反应机理（reaction mechanism）或反应历程。

19世纪中期，挪威化学家Guldberg和Waage在总结了大量工作和自己的实验基础上提出了质量作用定律（law of mass action）：化学反应速率与反应物的有效质量成正比（此处质量指浓度）。而只有基元反应才遵守质量作用定律。

简单来说，只有基元反应的化学反应速率才与反应物浓度（化学计量比作为幂次）的乘积成正比，只有基元反应才能根据反应直接写出速率方程。而总反应的速率方程一般不能直接根据反应物写出，只能通过实验手段测量。

（ 一个有趣的反推是：如果速率方程符合化学反应式，那么反应是否一定是基元反应？答案为否，例如经典的氢气与碘单质反应生成碘化氢的例子。 ）

在反应的速率方程中，各物质浓度项指数之代数和称为反应级数（order of reaction），例如如下速率方程：

$$
r= k[A]^a[B]^b
$$

反应的总级数为$(a+b)$，反应对于$A$的级数是$a$，反应对于$B$的级数是$b$。

有一些速率方程较为复杂，无法给出明确的反应级数。

速率方程中的$k$称为速率常数（rate constant），不同反应会有不同的速率常数，这与反应本身性质、温度和催化剂等有关。

11.4 具有简单级数的反应

本节介绍具有简单级数的反应的相关性质，详细的计算均略去，只给出对应结果。

凡是反应速率只与物质浓度的一次方成正比者称为一级反应（first order reaction），如放射性元素的衰变反应、五氧化二氮的分解、分子重排和蔗糖水解反应（准一级）。

设某一级反应：

$$
\begin{aligned} &A \quad\overset {k_1}\rightarrow &&P \[3mm]
t=0 \quad c_A^0&=a \quad &&c_P^0=0 \[3mm]
t=t \quad c_A&=a-x \quad &&c_P=x\end{aligned}
$$

则有：

$$
\frac {dx}{a-x} = k_1dt
$$

不定积分得：

$$
ln(a-x) = -k_1t + constant
$$

定积分得：

$$
\ln \frac {a}{a-x} = k_1t
$$

半衰期为：

$$
t_{1/2} = \frac {\ln 2}{k_1} = \frac {0.6931}{k_1}
$$

可见，一级反应的半衰期与反应物的浓度无关。

反应速率和物质浓度的二次方成正比者称为二级反应（second order reaction）。二级反应最为常见，如乙烯、丙烯等二聚、乙酸乙酯的皂化和甲醛的热分解等。

设某二级反应：

$$
\begin{aligned} &A\ \quad+ &&B \quad\overset {k_2}\rightarrow &&P \[3mm]
t=0 \quad &a &&b\quad &&0 \[3mm]
t=t \quad &a-x \quad &&b-x &&x\end{aligned}
$$

则有：

$$
\frac {dx}{dt} = k_2(a-x)(b-x)
$$

$a$和$b$可以相等也可以不等，均可以计算出相应的结果，不妨令$a=b$，则做定积分可得：

$$
\frac {1}{a-x} - \frac {1}{a} = k_2t
$$

半衰期为：

$$
t_{1/2} = \frac {1}{k_2a}
$$

二级反应的半衰期与反应物的起始浓度成反比。

反应速率与物质浓度的三次方成正比者称为三级反应（third order reaction）。三级反应为数不多，人们熟知的几个反应均与一氧化氮有关，分别是$NO$与$Cl_2,Br_2,O_2,H_2,D_2$的反应。

具体的速率方程表达式与上式同理，在此略去。

反应速率与物质浓度无关者称为零级反应（zeroth order reaction），反应总级数为零的反应并不多，已知的零级反应中主要是表面催化反应。

设某反应的速率方程为：

$$
r= kc_A^{\alpha}c_B^{\beta}
$$

该反应的级数应为$\alpha+\beta$，如果大大增加B的浓度，以致反应过程中B的浓度变化很小，则可把$c_B^{\beta}$当成常数并入速率常数$k$中。

因此该反应就变为了$\alpha$级反应，称为准$\alpha$级反应（pseudo α order reaction）。通常为了保证反应是准一级的，一种反应物的浓度至少需要过量40倍以上。

动力学方程都是根据大量的实验数据或用拟合法来确定的，确定反应级数和速率常数的常用方法有如下几种：

• 积分法。假定一组速率方程的幂次，然后求得积分项，并对$t$作图，若得到一条直线，就说明最初的假定正确。
• 微分法。先作$c-t$图，在多个点求切线斜率获得$r$，然后再作$\lg r - \lg c$图，斜率即为反应级数（或与级数相关）。
• 半衰期法。以不同的起始浓度开始实验，获得半衰期后即可计算出反应级数。
• 改变物质数量比例的方法。保持其他反应物浓度不变，只把其中一种物质浓度加大一倍，观察反应速率改变的倍率。

11.5 几种典型的复杂反应

如果一个反应是由两个以上的基元反应以各种方式相互联系起来的，那么这种反应就是复杂反应。本节介绍几种典型的复杂反应，详细的计算过程均略去，只给出对应结果。

• 对峙反应。在正、反两个方向上都能进行的反应称为对峙反应（opposing reaction），或称可逆反应。
  对于最简单的1-1级对峙反应而言，净的右向反应速率取决于正向减逆向反应速率的总结果，且达到平衡时速率为0，综合两个条件可以解出：$k_1=\frac {x_{eq}}{ta} \ln \frac {x_{eq}}{x_{eq}-x}$。
• 平行反应。反应物同时平行地进行两个或两个以上不同反应的反应称为平行反应（parallel reaction）。
  考虑平行进行两个一级反应的情况，平行反应的总速率为两个平行反应的速率之和，积分求得：$\ln \frac {a}{a-x} = (k_1+k_2)t$。因此发现，两个平行的一级反应的微分式和积分式与简单一级反应基本相同，不过速率常数变为两个平行反应的速率常数的和。
  如果两个平行反应均为二级反应，计算可得，两个反应的速率之比应为产物的数量之比：$\frac {k_1}{k_2} = \frac {x_1}{x_2}$。
• 连续反应。前一步的反应产物为下一步反应物，如此依次连续进行，这种反应就称为连续反应（consecutive reaction）。连续反应的典型特征是中间产物的浓度在反应过程中出现最大值。
  对于复杂的连续反应，要求出反应过程中各物质对于时间$t$的关系十分困难，往往需要一些近似方法。

11.6 基元反应的微观可逆性原理

对于上文提到的对峙反应，平衡时其基元反应的正向反应速率与逆向反应速率必须相等，这一原理称为精细平衡原理（principle of detailed balance）。从理论上讲，精细平衡原理是微观可逆性（microscopic reversibility）对大量微观粒子构成的宏观系统相互制约的结果。

微观可逆性意味着：基元反应的逆反应一定也是基元反应，且逆过程的途径和正反应相同，只是方向相反。

11.7 温度对反应速率的影响

历史上，van’t Hoff曾根据实验事实总结出一条近似规律，称为van’t Hoff近似规则：温度每升高10K，反应速率增加2-4倍。

$$
\frac {k_{T+10K}}{k_T} = 2 \sim 4
$$

这一规则可以用于温度对反应速率影响的粗略估计。

Arrhenius在研究了许多气相反应的速率后，提出了活化能的概念，并给出了反应速率常数与温度之间的依赖关系：

$$
k = A e^{-\frac {E_a}{RT}}
$$

上式称为Arrhenius公式，式中$k$为温度$T$时的速率常数，$A$为指前因子（pre-exponential factor），$E_a$是表观活化能（apparent activation energy，通常直接简称为活化能）。

对该式取对数得：

$$
\ln k =\ln A - \frac {E_a}{RT}
$$

假定$A$和$T$无关，则得到微分形式：

$$
\frac {d\ln k}{dT} = \frac {E_a}{RT^2}
$$

这种形式的公式在前文热力学部分中也多次出现，例如van’t Hoff公式：

$$
\frac {d\ln K^{\ominus}}{dT} = \frac {\Delta_rH^{\ominus}_m}{RT^2}
$$

根据Arrhenius公式和van’t Hoff公式发现，温度改变对反应的影响各有不同：由于$E_a$恒正，所以当$T$增大时，$k$也始终增大；而$\Delta_rH_m^{\ominus}$的符号决定了$K^{\ominus}$和$T$的关系。这两点并不矛盾，因为这两个公式分别是从动力学和热力学来考虑的，热力学中考虑反应进行的程度是在$t \rightarrow \infin$条件下的，而动力学则考虑反应速率的变化。一般来说，只要一个反应的平衡转化率没有低到没有生产价值的情况下， 速率因素总是矛盾的主要方面。

总反应与温度的关系可以分为以下几种类型：

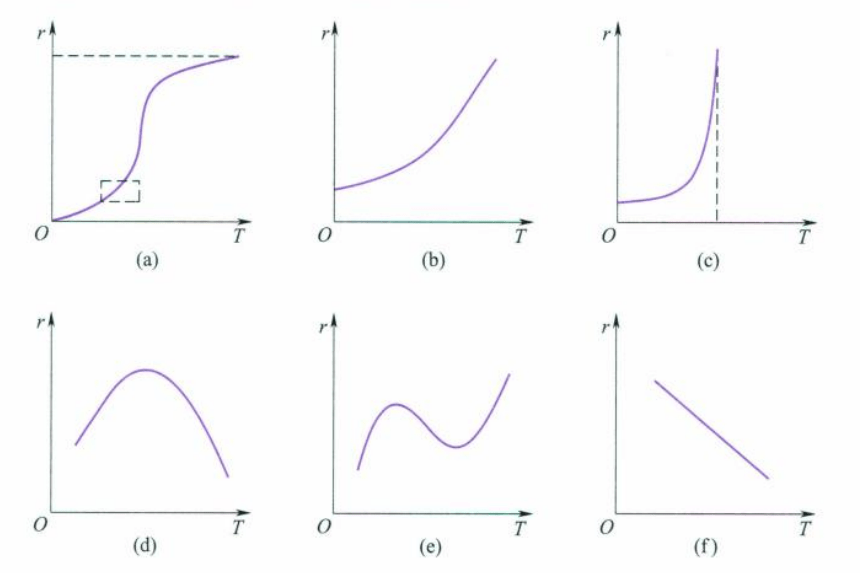
图(a)为根据Arrhenius公式绘制的S形曲线，当$T \rightarrow 0$时，$r \rightarrow 0$；当$T \rightarrow \infin$时，$r$有定值。图(b)是图(a)虚线部分，许多反应都是这一类型。图©对应的是总反应中含有爆炸性的反应，所以反应速率在某一温度处急速上升。

图(d)常见于一些受吸附速率控制的多相催化反应或者酶催化反应，随温度升高催化剂活性开始降低而产生先升后降的曲线形状。图(e)类型的反应可能随温度升高发生副反应，因此使反应速率复杂化。图(f)是比较反常的反应，例如一氧化氮氧化为二氧化氮的反应。

Arrhenius公式在一定温度范围内与实验结果基本相符，如果作$\ln k - \frac 1T$图像，根据Arrhenius公式，得一条直线，其斜率为$-E_a/R$：

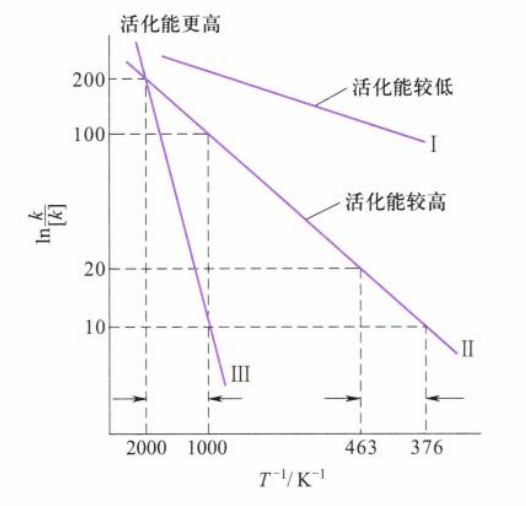
从图中可以看出，斜率绝对值越大的曲线，对应的活化能也越大。活化能越大的反应受温度影响也越大，升高温度对活化能大的反应有利。

11.8 关于活化能

对于复杂反应或实验温度范围大的反应，若作$\ln k - \frac 1T$图并没有得到一条很好的直线，这说明反应的活化能$E_a$实际上与温度有关。

对于基元反应，Tolman曾证明：

$$
E_a = \overline E^* - \overline {E}_R
$$

式中$\overline E^*$表示能发生反应分子的平均能量，$\overline E_R$表示所有反应物分子的平均能量，$E_a$为这两个统计平均能量的差值。

也就是说对于基元反应，反应想要发生，反应物必须获得足够的能量才能越过能垒变成产物，这个能垒就是活化能。

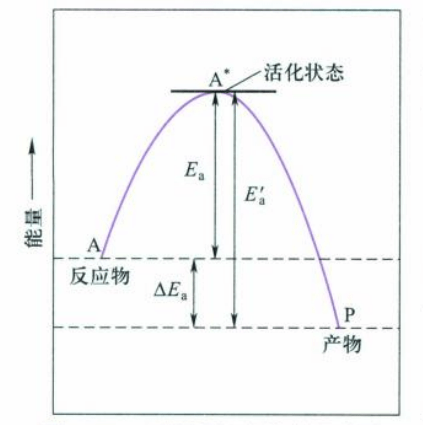
对于非基元反应，$E_a$的物理意义就不那么明确。通过推导得到，复杂反应的活化能仅是各基元反应活化能的组合，这是$E_a$称为该总反应的表观活化能。

既然$E_a$与温度有关，那么以$\ln k$对$1/T$作图就无法得到一条直线，所以我们需要将Arrhenius公式做修正：

$$
k = A_0T^m \exp (-\frac {E_0}{RT})
$$

式中多了一个$T^m$项，相当是对Arrhenius公式的修正项。对上式变形还可得：

$$
\ln k = \ln A_0 + m\ln T - \frac {E_0}{RT}
$$

若以$\ln \frac {k}{T^m}$对$1/T$作图则可得一条直线，而如果$m\ln T$项值不大，则说明$E_a$仍可看作是与温度无关。

活化能除了用各种实验方法来获得外，还有一些从理论上预测活化能的方法：

• 对于一般基元反应，所需活化能约占化学键断裂能量的30%。
• 对于有自由基参加的基元反应，所需活化能约占化学键断裂能量的5.5%。
• 对于分子分裂为两个原子或自由基的反应，所需活化能等于键能。
• 对于自由基的复合反应，所需活化能可认为是0。

上述估计均为经验规则，非常粗糙，仅能作为参考。

11.9 链反应

化学动力学中有一类特殊的反应，只要用热、光、辐射或其他方法使反应引发，它便能通过活性组分相继发生一系列的连续反应，称为链反应（chain reaction）。

链反应包括三个基本步骤：链开始、链传递、链终止。

根据链的传递方式不同，可将链反应分为直链反应（straight chain reaction）和支链反应（branched chain reaction）。

典型的直链反应如$H_2$和$Cl_2$的反应，反应过程中生成活性很高的自由基$H·$和$Cl·$。对于此类反应，若想严格计算各物种浓度与时间的关系，需要许多微分方程的联立求解，这是很难办到的，所以有必要采取一些近似方法简化计算。

由于自由基等中间产物极活泼，它们参加许多反应，但浓度低、寿命短，所以可认为在反应稳定后，中间产物的浓度基本上不随时间变化，这种近似方法称为稳态近似法（steady state approximation method，简称SS近似法）。若以氢气和氯气的反应为例，则：

$$
\frac {d[Cl·]}{dt} = \frac {d[H·]}{dt} =0
$$

稳态近似法只是一种近似方法，实际上在封闭系统中，中间产物浓度很难保持不变，但是应用这种方法确能解决很多问题。

氧气和氢气的反应属于支链反应，在一定条件下会发生爆炸。由于支链产生的自由基快速扩大反应而发生爆炸则称为支链爆炸；由于反应放热而使反应进一步加速而发生保证称为热爆炸。

11.10 拟定反应历程的一般方法

该部分非本书讨论重点，故略去。

总结

本章不少内容都是无机里的知识，重点在于简单级数反应的相关性质和应用，即对于复杂反应的讨论。