《物理化学》章末总结12

第十二章是化学动力的第二部分，介绍了碰撞理论、过渡态理论、单分子Lindermann理论等。本章数理推导非常多而繁复，本篇post会省略大部分具体的推导细节。

第十二章 化学动力学基础（二）

（ 正式开始前先闲聊一点，化学动力学这种内容是绝对少不了计算推导的，而本章相较上一章的计算强度又更高一些。但是平心而论无论是老师课堂教学还是学生自己学习，都不会在推导过程上下太多功夫，毕竟绝大多数人应该不会喜欢对着好几页复杂的公式模型一算算好几个小时吧。

但是这种做法存在着潜在的问题：有些东西不自己推导一遍是get不到精髓所在的。实际上如果去掉计算推导部分，只看定性结论的话，本章较无机化学中的反应动力学内容几乎没什么进一步扩充，仍然是那些老生常谈的理论。我自己在写post的时候也是面临着同样的问题，只给结论会显得浅尝辄止，写出计算细节则会耗费大量时间。

当然我并不是在说就必须得把计算过程完完全全算一遍，上文里我想强调的是计算过程中的一些细节，包括建模时所做的一些近似和忽略，设置的一些条件等等，了解这些细节可能会对整个理论的理解有很好的帮助。 ）

12.1 碰撞理论

碰撞理论是20世纪初在气体分子动理论的基础上发展起来的，该理论认为，发生化学反应的先决条件是反应物分子的碰撞接触，但是只有分子的相对平动能在分子连心线上的分量超过临界值的分子对才能发生反应。

满足条件的碰撞称为有效碰撞（effective collision），碰撞理论的关键在于得到分子的碰撞频率（$Z$）和有效碰撞在总碰撞中占比（$q$），即可求得反应速率和反应常数。

下文介绍简单碰撞理论（simple collision theory），因为该理论把分子的反应抽象为硬球碰撞。

根据气体分子动理论（见第一章）可给出运动的A分子和B分子单位时间内的碰撞频率：

$$
Z_{AB} = \pi d_{AB}^2 L^2 \sqrt {\frac {8RT}{\pi\mu}} c_Ac_B
$$

（ 现在回头看看第一章，我还有空刷Atkins，现在是碰都不碰了，令人感概。 ）

式中$d_{AB}$代表A分子和B分子的半径和；$\pi d_{AB}^2$称为碰撞截面；$\mu$为折合摩尔质量。

根据Boltzmann公式，具有能量$E$的活性分子在总分子中占比为：

$$
q=e^{-E/RT}
$$

因此可以计算反应速率，反应速率即为有效碰撞发生的速率：

$$
\begin {aligned} r &= -\frac {dc_A}{dt} = \frac {Z_{AB}}{L} \cdot q \[3mm] & = \pi d_{AB}^2L\sqrt {\frac {8RT}{\pi\mu}}e^{-E/RT}c_Ac_B = kc_Ac_B \end{aligned}
$$

因此速率常数也自然得到。

$$
k = \pi d_{AB}^2L\sqrt {\frac {8RT}{\pi\mu}}e^{-E/RT} = Ae^{-E/RT}
$$

式中$A$称为频率因子。

从上式就得到了Arrhenius公式的形式，因此碰撞理论很好的解释了Arrhenius公式。

从微观上考虑，分子的能量包含其动能和势能，而两个硬球碰撞时球心连线方向上的动能分量才是反应能否发生的判据。

分子的碰撞并不一定是对心碰撞，因此需要考虑硬球碰撞的截面，也就是微观上的反应截面。如果考虑反应截面的表达式，再给出简单碰撞理论的反应速率常数$k_{SCT}$：

$$
k_{SCT} = \pi d_{AB}^2 L\sqrt {\frac {8k_BT}{\pi \mu}} e^{-\epsilon_c/k_BT}
$$

根据实验活化能的定义：

$$
E_a = RT^2 \frac {d\ln k(T)}{dT}
$$

因此可得$E_a$和$E_c$的关系：

$$
E_a = RT^2 \left(\frac 1{2T} + \frac {E_c}{RT^2} \right) = E_c + \frac 12 RT
$$

如果$E_c \gg \frac 12RT$，则认为$E_a \approx E_c$，但是两者物理意义并不同，$E_c$称为临界能或阈能（threshold energy）。

对于许多常见反应，上述理论计算所得的$k(T)$值和$A$值与实验值基本相符，但是也有很多例外，有时计算结果比实际情况大很多。

人们在公式中增加一个校正因子$P$，用于修正误差，称为概率因子或空间因子（steric factor）。

$$
k(T) = PA \exp \left(\frac {-E_a}{RT} \right)
$$

空间因子的加入主要是用于修正分子在反应时的取向和基团空间位阻的影响。

12.2 过渡态理论

过渡态理论（transition state theory, TST）又称活化络合物理论，这个理论是1935年后由Eyring、Polanyi等人在统计力学和量子力学发展的基础上提出来的。

该理论认为化学反应不是通过简单碰撞完成的，在形成过渡态的过程中要考虑分子的内部结构和内部运动，并分析整个系统的势能。活化络合物与反应物分子之间建立化学平衡，反应的速率由活化络合物转化为产物的速率来决定。

过渡态理论原则上提供了一种计算反应速率的方法，只要知道分子的某些基本物性，即可计算某反应的速率常数，故该理论也成为绝对反应速率理论（absolute rate theory, ART），即通过该理论可从理论上完全计算反应速率而不需实验数据。

原子间相互作用表现为原子间有势能$E_p$存在，势能的值是原子的核间距$r$的函数。对于线性活化络合物，则其势能变化可用三维空间中的曲面表示，如下例所示：

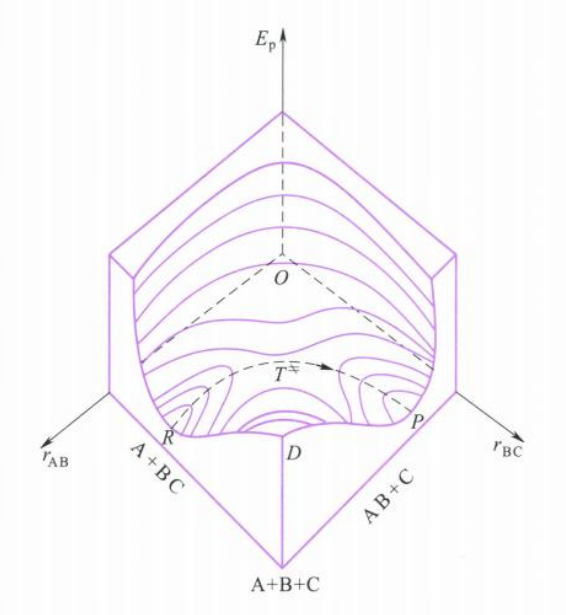
类似于等高线地形图，势能图上也有“山峰”和“山谷”，连接反应起点和终点的山脊的顶点是势能面上的鞍点（saddle point），此处的势能$T^{\neq}$即为活化络合物的势能。

反应通过鞍点前进是能量最低的通道，但也必须越过势垒$E_b$，$E_b$是活化络合物与反应物两者最低势能之差值，两者零点能之间差值为$E_0$。

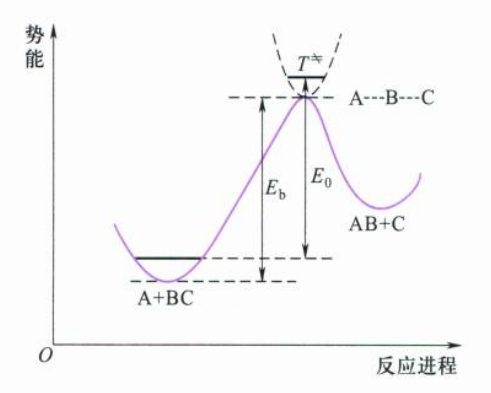
过渡态理论认为活化络合物向产物转化是整个反应的决速步骤。

$$
r = -\frac {d[A\cdots B\cdots C]^{\neq}}{dt} = \nu [A\cdots B\cdots C]^{\neq} = \nu K_c^{\neq} [A][BC]
$$

式中$\nu$为不对称伸缩振动的频率。如果我们能求得$K_c^{\neq}$，就能再求得速率常数。通过一系列统计力学计算可知：

$$
k = \nu K_c^{\neq} = \frac {k_BT}{h} \frac {f^{\neq}’}{f_A f_{BC}} \exp \left(-\frac {E_0}{RT} \right)
$$

上式即为统计热力学方法处理的过渡态理论计算速率常数的表达式，该公式可进一步推广用于其他基元反应：

$$
k = \frac {k_BT}{h} \frac {f^{\neq}’}{\prod_B f_B} \exp \left(-\frac {E_0}{RT} \right)
$$

任何分子都有3个平动自由度，线性分子有2个转动自由度，（3n-5）个振动自由度；非线性分子有3个转动自由度，（3n-6）个振动自由度。在活化络合物中，有一个不对称伸缩振动自由度用于其分解，则总的振动自由度要比正常分子少一个。

例如，对于如下反应：

$$
A(N_A)+B(N_B) \rightleftharpoons [A \cdots B]^{\neq}(N_A+N_B)
$$

式中$N_A,N_B$为对应分子的原子数，所有分子均为非线性多原子分子，则有：

$$
k = \frac {k_BT}{h} \frac {[f_t^3 f_r^3 f_v^{N_A+N_B-7}]^{\neq}}{(f_t^3f_r^3f_v^{3N_A-6})_A (f_t^3 f_r^3 f_v^{3N_B-6})_B} \exp \left(-\frac {E_0}{RT} \right)
$$

如果我们从热力学角度出发，通过热力学函数的变化值来计算速率常数，我们也能相应得到：

$$
k = \frac {k_BT}{h} K_c^{\neq} = \frac {k_BT}{h}(c^{\ominus})^{1-n} \exp \left[-\frac {\Delta_r^{\neq}G_m^{\ominus}(c^{\ominus})}{RT} \right]
$$

$$
k = \frac {k_BT}{h}(c^{\ominus})^{1-n} \exp \left[\frac {\Delta_r^{\neq}S_m^{\ominus}(c^{\ominus})}{R} \right] \exp \left[-\frac {\Delta_r^{\neq}H_m^{\ominus}(c^{\ominus})}{RT} \right]
$$

上式中热力学量分别为标准摩尔活化Gibbs自由能、标准摩尔活化熵、标准摩尔活化焓。

据此我们也能发现，活化熵的部分实际上是指前因子A的一部分，而活化焓实际上近似等于活化能（温度不太高时近似成立）。

12.3 单分子反应理论

理论上，单分子反应（unimolecular reaction）应该是由一个分子所实现的基元反应，但是一个孤立的基态分子不能自发进行反应，所以分子的能量实际上是通过相同分子间的碰撞而实现活化的。

1922年，Lindemann等人提出了单分子反应的碰撞理论，认为单分子反应是通过相同分子间的碰撞而达到活化状态的，而获得足够能量的活化分子并不立即分解，需要一个分子内部的能量传递过程，即产生一段停止时间（time lag）。其机理可表示如下：

$$
\begin{aligned} &A \longrightarrow P \[3mm]
(1) &A + A \overset{k_1}{\underset{k_{-1}} {\leftrightharpoons}} A^* + A \[3mm]
(2) &A^* \overset{k_2}\longrightarrow P \end{aligned}
$$

式（1）并不是化学变化，而是使分子活化的传能过程。分子在活化后可能发生反应，也有可能消活化（deactivation）而再变为普通分子。则分子活化的净速率为：

$$
\frac {d[A^]}{dt} = k_1[A]^2 - k_{-1}[A][A^] - k_2[A^*]
$$

利用微态近似假设：

$$
\frac {d[A^*]}{dt} = 0
$$

由此解得：

$$
[A^*] = \frac {k_1[A]^2}{k_{-1}[A]+k_2}
$$

$$
r = k_2[A^*] = \frac {k_1k_2[A]^2}{k_{-1}[A]+k_2}
$$

上式即为Lindemann单分子理论所推出的结果，按此结果可对单分子反应的情况进行分析。

当$A^$转化为产物的速率远大于$A^$的消活化速率时，即$k_2 \gg k_{-1}[A]$，反应表现为二级反应，$r=k_1[A]^2$。

当$A^*$转化为产物的速率远小于消活化速率时，即$k_2 \ll k_{-1}[A]$，反应表现为一级反应，$r=(k_2k_1/k_{-1}) \cdot [A]$。

Lindemann理论在定性上基本符合实际，但是在定量上往往与实验结果有偏差，因此不少学者都对其进行修正，如20世纪50年代提出的RRKM（Rice-Ramsperger-Kassel-Marcus）理论，将Lindemann理论和过渡态理论结合起来，得到了与实验值符合较好的结果。

12.4 分子反应动态学简介

本章简要介绍了分子反应动态学，从微观角度上研究态-态反应，本章内容超出课程要求范围，故略去。

12.5 在溶液中进行的反应

溶液中的反应与气相反应相比，最大的不同是有溶剂分子的存在，同一个反应在气相和溶液中进行可能会有不同的速率，甚至不同的历程，得到不同的产物，这些都是溶剂效应引起的。本节简要介绍溶剂对反应的几个影响因素。

• 笼效应（cage effect）。反应分子在溶液中被溶剂分子包围，可以认为溶剂分子在反应分子周围形成了一个笼，分子要想碰撞发生反应必须穿过周围的溶剂分子。而当反应分子碰撞时，笼效应会让反应分子在溶剂笼中反复多次碰撞，直到反应分子从笼中挤出。因此溶剂分子的存在虽然减少了远距离分子的接触碰撞，但是也加强了近距离分子的重复碰撞。
• 原盐效应（primary salt effect）。由过渡态理论和Debye-Hückel极限公式导出：$\lg k/k_0 = 2z_Az_B A\sqrt I$。即反应物的电荷乘积的正负会影响反应速率与离子强度的关系，对于非电解质，则反应速率与溶液离子强度无关。

12.6 快速反应的几种测试手段

单分子反应和双分子反应的速率常数都极大，传统的测量反应速率的物理化学方法不能测量如此快速反应的速率，因此随着科学技术的发展，对快速反应动力学的研究方法也在不断发展，如弛豫法、场脉冲法、闪光光解法和动力学波谱法等。

详细介绍略去。

12.7 光化学反应

只有在光的作用下才能进行的化学反应或由于化学反应产生的激发态粒子在跃迁到基态时能放出光辐射的反应称为光化学反应（photochemical reaction）。

光化学反应与热反应有许多不同，例如等温等压下，热反应总是向系统的Gibbs自由能降低的方向进行，但许多光化学反应却能使系统的Gibbs自由能升高。因为光为系统提供了能量。

再如热反应的活化能来源自分子的碰撞，而光化学反应的活化能来源于光子的能量；光反应的活化能普遍较热反应小；光作用下的化学反应是激发态分子的反应，而非光作用下的化学反应通常是基态分子的反应。以上都是热反应与光化学反应的不同。

光化学从物质吸收光子开始，此过程统称光化反应的初级过程（primary process），它使反应物分子或原子中的电子从基态跃迁到激发态。

初级过程的产物可以进行一系列的刺激过程（secondary process），如猝灭（quenching）、荧光（fluorescence）、磷光（phosphorescence）等。

由于激发态不稳定，寿命很短，所以如果切断光源，荧光立刻停止，但是磷光在切断光源后仍能延续若干秒，这是因为发磷光时常需经过介稳状态。

光化学中有一些基本规律，如光化学第一定律，又称Grotthus-Draper定律，其表述为只有被分子吸收的光才能引起分子的光化学反应。

光化学第二定律是指一个反应分子吸收一个光子而被活化，又称Stark-Einstein定律，现在由于激光在光化学反应的使用越来愈多，也有不符合Stark-Einstein定律的反应出现。

衡量光化学反应的效率，可用量子产率（quantum yield）$\phi$表示：

$$
\phi = \frac {反应物分子消失数目}{吸收光子数目} = \frac {反应物消失的物质的量}{吸收光子物质的量}
$$

也可用生成的产物分子数目来定义量子产率：

$$
\phi ’ = \frac {产物分子生成数目}{吸收光子数目} = \frac {产物生成的物质的量}{吸收光子物质的量}
$$

由于受反应式计量系数的影响，$\phi$和$\phi’$的数值很可能不等，因此可用反应速率和吸收光子速率来定义量子产率：

$$
\phi = \frac {r}{I_a}
$$

光化学反应初级过程的反应速率一般只与入射光的强度有关，而与反应物浓度无关，所以初级光化学反应对反应物呈零级反应。

一些光化学反应可以建立光化学平衡，这种稳态称为光稳定态（photo stationary state）。光化学反应对温度不敏感是因为光化学的初级过程与吸收光的强度有关，而次级过程又常涉及自由基反应，其活化能不大，因此受温度影响不大。

12.8 化学激光简介

激光是一种单色、亮度高、相干性好、方向性好的相干光束。受激辐射、受激吸收及自动辐射等是电磁波与物质相互作用的三种基本现象，激光也由此产生。

本章内容略去。

12.9 催化反应动力学

能加快反应速率而不改变反应总的标准摩尔Gibbs自由能变化的物质称为催化剂（catalyst），相关过程称为催化作用（catalysis）。

催化剂能加快反应到达平衡的速率，是由于改变了反应历程，降低了活化能，催化剂不影响化学平衡。催化剂有特殊的选择性，某一类反应只能用某些催化剂来进行催化。

本节介绍几种催化过程的反应动力学。

• 均相酸碱催化。酸催化反应包含催化剂分子把质子转移给反应物的步骤，因此催化剂的效率常与酸强度有关。实验表明，$k_a = G_aK_a^{\alpha}$。
• 络合催化。又称配位催化。反应分子可与配位数不饱和的络合物直接配位，然后配体转移插入到相邻的金属-配体键中，使得空位恢复，然后又可重新进行络合和插入反应。
• 酶催化反应。对于酶催化反应动力学，有Michaelis-Menten机理，指出酶（E）和底物（S）先形成中间化合物（ES），然后中间化合物再进一步分解为产物，并释放酶。有$[ES] = \frac {k_1[E][S]}{k_{-1}+k_2} = \frac {[E][S]}{K_M}$，$r=\frac {d[P]}{dt} = k_2[ES]=\frac {k_2[E_0][S]}{K_M + [S]}$。该结果与事实相符。
• 自催化反应。反应开始后逐渐形成并积累了某种产物/中间体，其具有催化功能，使反应经过一段诱导期后速率大大加快，称为自催化作用（autocatalysis）。有些自催化反应可能使反应系统中某些物质浓度随时间发生周期性变化，即发生化学振荡（chemical oscillation）。具体的动力学过程较为复杂，在此略去。

总结

本章为动力学部分二，介绍了有关反应的具体机理的理论，该部分的详细计算较为复杂，且理论发展时间短，有许多过程与机理尚不明晰，所以仍以定性结论为主。