《Quantum Chemistry》章末总结6

第六章是刚性转子和转动光谱。

Chapter 6 The Rigid Rotator and Rotational Spectroscopy

The rotation of a diatomic molecule can be described by a rigid rotator, which is like a rotating dumbbell. Using the concept of a reduced mass, we can picture the rotator as a body of reduced mass $\mu$ rotating about a fixed center.

This problem lends itself naturally to spherical coordinates, and the wave functions are functions of $\theta$ and $\phi$, the two angles in spherical coordinates. The wave functions are called spherical harmonics and occur in many problems involving a fixed center.

Solving the Schrödinger equation for a rigid rotator is a fairly lengthy process, and so in most of this chapter we shall simply present and discuss the energies and the corresponding wave functions.

（ 描述转动问题会很自然地引入球坐标系，后面在解氢原子时也是在球坐标系下进行的。 ）

6.1 The Energy Levels of a Rigid Rotator Are $E=\hbar^2J(J+1)/2I$

In this section, we will discuss a simple model for a rotating diatomic molecule. The model consists of two point masses $m_1$ and $m_2$ at fixed distances $l_1$ and $l_2$ from their center of mass (cf. Figure 6.1).

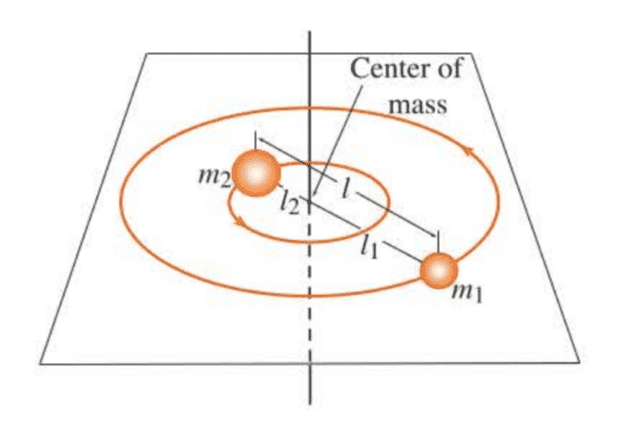
Because the distance between the two masses is fixed, this model is referred to as the rigid-rotator model. Even though a diatomic molecule
vibrates as it rotates, the vibrational amplitude is small compared with the bond length, so considering the bond length fixed is a good approximation.

（ 对于双原子分子，在考虑转动时，可以忽略振动对于键长的微小影响，即把双原子分子当成刚性转子处理。 ）

Let the molecule rotate about its center of mass at a frequency of $\nu_{rot}$ cycles per second. The kinetic energy of the rigid rotator is:

$$
\begin{aligned} T &=\frac 12m_1v_1^2+\frac 12m_2v_2^2=\frac 12(m_1l_1^2+m_2l_2^2)\omega^2 \[3mm] &= \frac 12I\omega^2 \end{aligned}
$$

where $I$, the moment of inertia, is given by:

$$
I=m_1l_1^2+m_2l_2^2=\mu l^2
$$

where $l=l_1+l_2$ and $\mu$ is the reduced mass. We may consider the equation to be an equation for the moment of inertia of a single body of mass $\mu$ rotating at a distance $l$ from a fixed center. Thus, we have transformed a two-body problem into an equivalent one-body problem.

The angular momentum $L$ is:

$$
L=I\omega
$$

and the kinetic energy is:

$$
T=\frac {L^2}{2I}
$$

There is no potential energy term because in the absence of any external forces the energy of the molecule does not depend on its orientation in space. The Hamiltonian operator of a rigid rotator is therefore just the kinetic energy operator:

$$
\hat H=\hat T=-\frac {\hbar^2}{2\mu}\nabla^2 \quad (r\ constant)
$$

We need to convert $\nabla^2$ from cartesian coordinates to spherical coordinates:

$$
\nabla^2=\frac 1{r^2}\frac {\partial}{\partial r} \left( r^2\frac {\partial}{\partial r}\right){\theta,\phi}+\frac 1{r^2\sin\theta}\frac {\partial}{\partial \theta} \left(\sin\theta\frac {\partial}{\partial \theta} \right){r,\phi}+\frac 1{r^2\sin^2\theta} \left(\frac {\partial^2}{\partial\phi^2} \right)_{r,\theta}
$$

The rigid rotator is a special case where $r$ is equal to a constant, $l$, so it becomes:

$$
\nabla^2=\frac 1{l^2\sin\theta}\frac {\partial}{\partial \theta} \left(\sin\theta\frac {\partial}{\partial \theta} \right)+\frac 1{l^2\sin^2\theta} \frac {\partial^2}{\partial\phi^2} \quad (r\ constant)
$$

And now we obtain:

$$
\hat H=-\frac {\hbar^2}{2I} \left[\frac {1}{\sin\theta}\frac {\partial}{\partial \theta} \left(\sin\theta \frac {\partial}{\partial \theta} \right)+\frac 1{\sin^2\theta} \left(\frac {\partial^2}{\partial \phi^2} \right) \right]
$$

$$
\hat L^2=-\hbar^2 \left[\frac {1}{\sin\theta}\frac {\partial}{\partial \theta} \left(\sin\theta \frac {\partial}{\partial \theta} \right)+\frac 1{\sin^2\theta} \left(\frac {\partial^2}{\partial \phi^2} \right) \right]
$$

The orientation of a rigid rotator is completely specified by the two angles $\theta$ and $\phi$, so rigid-rotator wave functions depend upon only these two variables. So the Schrödinger equation for a rigid rotator reads:

$$
\hat H Y(\theta,\phi)=EY(\theta,\phi)
$$

To solve the equation, we again use the method of separation of variables:

$$
Y(\theta,\phi)=\Theta(\theta)\Phi(\phi)
$$

We find:

$$
\frac {\sin\theta}{\Theta(\theta)}\frac {d}{d\theta} \left(\sin\theta\frac {d\Theta}{d\theta} \right)+\beta \sin^2\theta+\frac 1{\Phi(\phi)}\frac {d^2\Phi}{d\phi^2}=0 \quad \left(\beta=\frac {2IE}{\hbar^2} \right)
$$

Because $\theta$ and $\phi$ are independent variables, we must have:

$$
\frac {\sin\theta}{\Theta(\theta)}\frac {d}{d\theta} \left(\sin\theta\frac {d\Theta}{d\theta} \right)+\beta \sin^2\theta = m^2
$$

and:

$$
\frac 1{\Phi(\phi)}\frac {d^2\Phi}{d\phi^2} = -m^2
$$

where $m^2$ is a constant.

The second equation contains only constant coefficients, it is relatively easy to solve:

$$
\Phi(\phi)=A_me^{im\phi} \quad and \quad \Phi(\phi)=A_{-m}e^{-im\phi}
$$

The requirement that $\Phi(\phi)$ be a single-valued function of $\phi$ is:

$$
\Phi(\phi+2\pi)=\Phi(\phi)
$$

With this, we obtain:

$$
\cos(2\pi m)\pm i \sin(2\pi m)=1
$$

which implies that $m=0,\pm1,\pm2,\cdots$. And:

$$
\Phi_m(\phi)=A_me^{im\phi} \quad m=0,\pm1,\pm2,\cdots
$$

We can find the value of $A_m$ by requiring that the $\Phi_m(\phi)$ be normalized, $A_m=(2\pi)^{-1/2}$.

（ 对于含$\Phi$的方程，易于给出它的解。根据函数单值性的要求，可以求得$m$的取值必须为整数。 ）

When we solve the first equation, it turns out naturally that $\beta$ must obey the condition:

$$
\beta=J(J+1) \quad J=0,1,2,\cdots
$$

It means:

$$
E_J=\frac {\hbar^2}{2I}J(J+1)=BJ(J+1) \quad J=0,1,2,\cdots
$$

where $B=\hbar^2/2I$ is called the rotational constant of the molecule.

Once again, we obtain a set of discrete energy levels. In addition to the allowed energies given by the equation, we also find that each energy level has a degeneracy $g_J$ given by:

$$
g_J=2J+1
$$

We’ll see later that this degeneracy is due to the fact that $m$ can take on the value $-J$ through $+J$.

（ 含$\Theta$的方程求解起来较为复杂，仍然是使用级数展开法，涉及到连带勒让德方程等，详细过程见相关量子力学教材。 ）

6.2 The Rigid Rotator Is a Model for a Rotating Diatomic Molecule

We will show in Section 6.7 that the selection rule for the rigid rotator says that transitions are allowed only from adjacent states or that:

$$
\Delta J=\pm1
$$

In addition to the requirement that $\Delta J=\pm1$, the molecule must also possess a permanent dipole moment to absorb electromagnetic radiation. Thus, $HCl$ has a pure rotational spectrum, but $N_2$ does not.

In the case of absorption of electromagnetic radiation, the energy difference is:

$$
\begin{aligned} \Delta E &= E_{J+1}-E_J=\frac {\hbar^2}{2I}[(J+1)(J+2)-J(J+1)] \[3mm] &=\frac {\hbar^2}{I}(J+1)=\frac {h^2}{4\pi^2I}(J+1) \quad J=0,1,2,\cdots \end{aligned}
$$

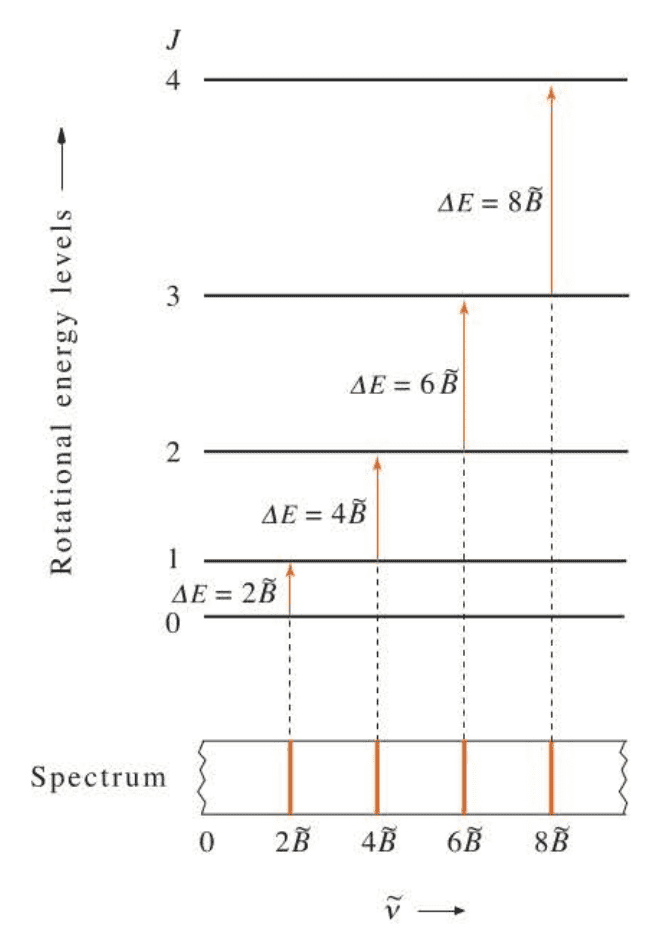
Using the Bohr frequency condition $\Delta E=h\nu_{obs}$ the frequencies at which the absorption transitions occur are:

$$
\nu_{obs}=\frac {h}{4\pi^2 I}(J+1) \quad J=0,1,2,\cdots
$$

The moment of inertia of a diatomic molecule typically ranges from $10^{-45}$ to $10^{-46},kg\cdot m^2$. Substituting $I=5\times10^{-46},kg\cdot m^2$ into the equation shows that the absorption frequencies are about $2\times10^{10}$ to $10^{11},Hz$. We see that these frequencies lie in the microwave region, and the study of rotational transitions in molecules is called microwave spectroscopy.

It is common practice in microwave spectroscopy to write the equation as:

$$
\nu_{obs}=2B(J+1) \quad J=0,1,2,\cdots
$$

where:

$$
B=\frac h{8\pi^2I}\ (Hz)
$$

is the rotational constant expressed in units of hertz.

Furthermore, the transition frequency is commonly expessed in terms of wave numbers rather than hertz:

$$
\tilde\omega_{obs}=2\tilde B(J+1) \quad J=0,1,2,\cdots
$$

where $\tilde B$ is the rotational constant expressed in units of wave numbers:

$$
\tilde B=\frac h{8\pi^2cI}\ (cm^{-1})
$$

We see that the rigid-rotator model predicts that the microwave spectrum of a diatomic molecule consists of a series of equally spaced lines with a separation of $2B,HZ$ or $2\tilde B,cm^{-1}$.

（ 刚性转子模型同样受到选律的限制，这意味着双原子分子转动光谱上的谱线都是等间距的。 ）

6.3 Rotational Transitions Accompany Vibrational Transitions

In the previous chapter, we showed that the vibrational motion of a diatomic molecule can be well approximated by a ha1monic oscillator, and in this chapter, we have just seen that the rotational motion of a diatomic molecule can be well represented by a rigid rotator. We combine these ideas and say that the rotational-vibrational motion of a diatomic molecule can be well approximated by the rigid rotator- harmonic oscillator model.

Within the rigid rotator-harmonic oscillator approximation, the rotational and vibrational energy of a diatomic molecule is given by:

$$
E_{v,J}= \left(v+\frac 12 \right)h\nu+BJ(J+1)
$$

or:

$$
\tilde E_{v,J}= \left(v+\frac 12 \right)\tilde \omega + \tilde BJ(J+1) \quad v,J=0,1,2,\cdots
$$

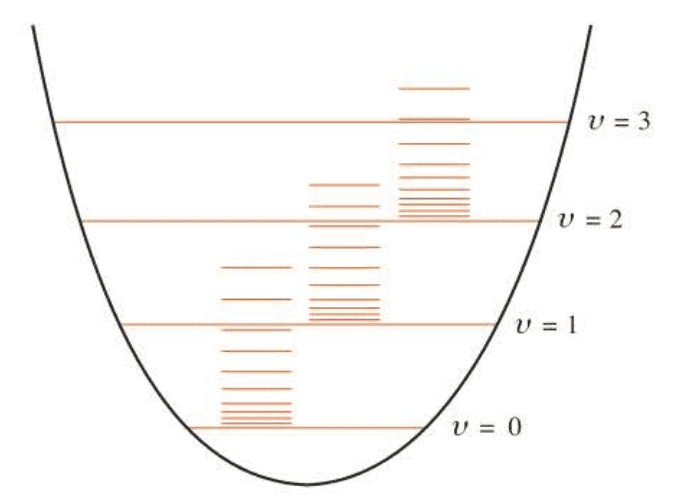
Typical values of $\tilde \omega$ and $\tilde B$ are of the order of $10^3,cm^{-1}$ and $1,cm^{-1}$, respectively, so the spacing between vibrational energy levels is about 100 to 1000 times the spacing between rotational levels.

When a molecule absorbs infrared radiation, the vibrational transition is accompanied by a rotational transition. The rotation-vibration spectrum of $HBr(g)$ is shown in Figure 6.4.

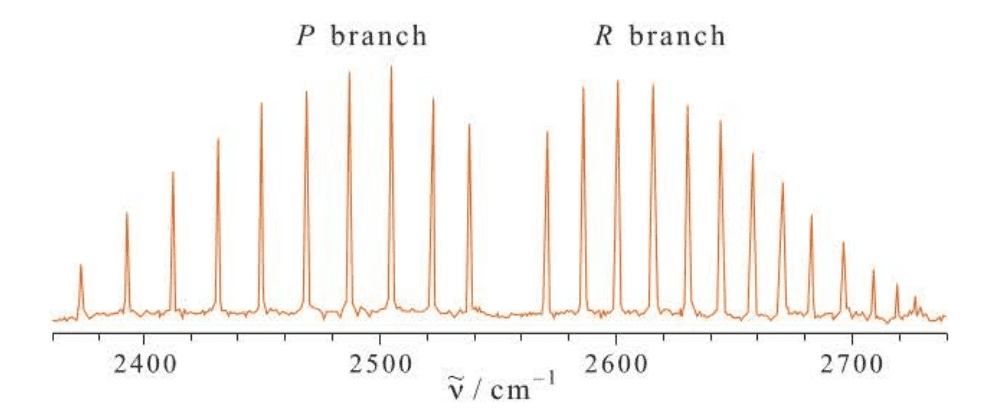
The gap centered around $2560,cm^{-1}$ corresponds to the missing line at $\tilde \omega$, because the transition $\Delta J=0$ is forbidden. On each side of the gap is a series of lines whose spacing is about $10,cm^{-1}$. The series toward the high-frequency side is called the R branch and is due to rotational transitions with $\Delta J=+1$. The series toward the low frequencies is called the P branch and is due to rotational transitions with $\Delta J=-1$.

（ 可以从图中看出，振动光谱谱线的能差远大于转动光谱谱线的能差，也就是说在发生振动能级跃迁的同时一定伴随着转动能级跃迁。 ）

But we also see several features we cannot explain. Close examination shows that the lines in the R branch are more closely spaced with increasing frequency and that the lines of the P branch become further apart with decreasing frequency. We will discuss the spacing of the lines in the R and P branches in the next section.

6.4 Rotation-Vibration lnteraction Accounts for the Unequal Spacing of the Lines in the P and R Branches of a Rotation-Vibration Spectrum

The energies of a rigid rotator-harmonic oscillator are given by:

$$
\tilde E_{v,J}=\tilde \omega \left(v+\frac 12 \right)+\tilde BJ(J+1)
$$

where $\tilde B=h/8\pi^2cI=h/8\pi^2c\mu l^2$.

Because the vibrational amplitude increases with the vibrational state (cf. Figure 6.3), we expect that $l$ should increase slightly with $v$, causing $\tilde B$ to decrease with increasing $v$. We will indicate the dependence of $\tilde B$ upon $v$ by using $\tilde B_v$ in place of $\tilde B$:

$$
\tilde E_{v,J}=\tilde \omega \left(v+\frac 12 \right)+\tilde B_vJ(J+1) \quad \left(\tilde B_v=\tilde B_e-\tilde \alpha_e \left(v+\frac 12 \right)\right)
$$

The dependence of $\tilde B$ on $v$ is called rotation-vibration interaction. If we consider a $v=0\rightarrow1$ transition, then the frequencies of the P and R branches will be given by:

$$
\begin{aligned} \tilde\nu_R(\Delta J=+1) &=E_{1,J+1}-E_{0,J} \[3mm] &=\frac 32\tilde \omega+\tilde B_1(J+1)(J+2)-\frac 12\tilde\omega-\tilde B_0J(J+1) \[3mm] &= \tilde\omega+2\tilde B_1+(3\tilde B_1-\tilde B_0)J+(\tilde B_1-\tilde B_0)J^2 \quad J=0,1,2,\cdots \end{aligned}
$$

and:

$$
\begin{aligned} \tilde\nu_P(\Delta J=-1) &=E_{1,J-1}-E_{0,J} \[3mm] &= \tilde\omega-(\tilde B_1+\tilde B_0)J+(\tilde B_1-\tilde B_0)J^2 \quad J=1,2,3,\cdots \end{aligned}
$$

Because the bond length increases with increasing $v$, $\tilde B_1<\tilde B_0$, and therefore the spacing between the lines in the R branch decreases and the spacing between the lines in the P branch increases with increasing $J$.

（ 由于振转相互作用的存在，振转光谱的P支谱线随波数减小，间隔实际上逐渐变大；R支谱线随波数增大，间隔实际上逐渐变小。 ）

6.5 The Lines in a Pure Rotational Spectrum Are Not Equally Spaced

We can find the line in a pure rotational spectrum aren’t exactly equally spaced as the rigid-rotator approximation predicts. The discrepancy can be resolved by realizing that a chemical bond is not truly rigid. As the molecule rotates more energetically (increasing $J$), the centrifugal force causes the bond to stretch slightly.

This small effect can be treated by perturbation theory (Chapter 8), and the end result is that the energy can be written as:

$$
E_J=\tilde BJ(J+1)-\tilde DJ^2(J+1)^2
$$

where $\tilde D$ is called the centrifugal distortion constant.

（ 高转动能级时，分子转动加剧，离心运动会使得化学键被拉长，我们引入离心畸变常数来描述离心对能量的影响。这意味着纯转动光谱也不是像刚性转子模型所显示的等间距光谱线。 ）

The frequencies of the absorption due to $J \rightarrow J+1$ transitions are given by:

$$
\begin{aligned} \tilde \omega &=E_{J+1}-E_J \[3mm] &=2\tilde B(J+1)-4\tilde D(J+1)^2 \quad J=0,1,2,\cdots \end{aligned}
$$

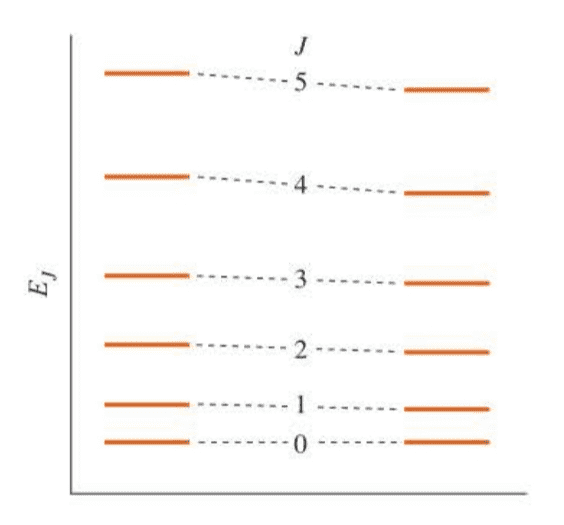
The rotational enegy level of a rigid rotator (left) and a nonrigid rotator (right).

6.6 The Wave Functions of a Rigid Rotator Are Called Spherical Harmonics

We can get the normalized solution to the rigid-rortator wave functions:

$$
Y_J^m(\theta,\phi)=i^{m+|m|} \left[\frac {(2J+1)}{4\pi}\frac {(J-|m|)!}{(J+|m|)!} \right]^{1/2} P_J^{|m|}(\cos\theta)e^{im\phi}
$$

With $J=0,1,2,\cdots$ and $m=0,\pm1,\pm2,\cdots,\pm J$. They are also the angular part of the hydrogen atomic orbitals, are given by $\Theta_j^m(\theta)\Phi_m(\phi)$.

（ 解方程的过程较为复杂，在此忽略，具体可参考量子力学教材。 ）

The $Y_J^m(\theta,\phi)$ form an orthonormal set:

$$
\int_0^{\pi}d\theta \sin\theta \int_0^{2\pi}d\phi Y_K^m(\theta,\phi)^*Y_{J’}^k(\theta,\phi)=\delta_{JJ’}\delta_{mk}
$$

Note that the $Y_J^m(\theta,\phi)$ are orthonormal with respect to $\sin\theta d\theta d\phi$ and not just $d\theta d\phi$. $\sin\theta d\theta d\phi$ is an area element on the surface of a sphere of unit radius. So the $Y_J^m(\theta,\phi)$ are orthonormal over a spherical surface and so called spherical hramonics.

In summary, the Schrödinger equation for a rigid rotator is:

$$
\hat HY_J^m(\theta,\phi)=\frac {\hbar^2J(J+1)}{2I}Y_J^m(\theta,\phi) \quad J=0,1,2,\cdots
$$

Because $\hat H=\hat L^2/2I$, we can write the expression of $\hat L^2$ and the eigenvalue equation for $\hat L^2$ is:

$$
\hat L^2Y_J^m(\theta,\phi)=\hbar^2J(J+1)Y_J^m(\theta,\phi)
$$

Thus, we see that the spherical harmonics are also eigenfunctions of $\hat L^2$ and that the square of the angular momentum can have only the values given by:

$$
L^2=\hbar^2J(J+1) \quad J=0,1,2,\cdots
$$

We shall discuss angular momentum more fully in Section 6.8.

6.7 The Selection Rule in the Rigid-Rotator Approximation Is $\Delta J=\pm1$

As we said when we discussed the selection rule for a harmonic oscillator in Section 5.12, the probability that a molecule makes a transition from one vibrational state to another when it is irradiated with electromagnetic radiation in the z direction is given by the square of an integral of the form:

$$
\langle v’|\mu_z|v \rangle =\int_{-\infin}^{\infin} dx\psi_{v’}(x)\mu_z(x)\psi_v(x)
$$

In the case of a rigid rotator, the transition dipole moment integral takes the form (we shall derive this result in Section 8.6):

$$
\langle J’,m’|\mu_z|J,m \rangle =\int_0^{2\pi}\int_0^{\pi}Y_{J’}^{m’}(\theta,\phi)^*\mu_zY_J^m(\theta,\phi) \sin\theta d\theta d\phi
$$

Using the fact that $\mu_z=\mu_0 \cos\theta$ gives:

$$
\langle J’,m’|\mu_z|J,m \rangle =\mu_0\int_0^{2\pi}\int_0^{\pi}Y_{J’}^{m’}(\theta,\phi)^*Y_J^m(\theta,\phi) \cos\theta \sin\theta d\theta d\phi
$$

Notice that $\mu_0$ must be nonzero for the transition moment to be nonzero. Thus, we have now proven our earlier assertion that a molecule must have a permanent dipole moment for it to have a pure rotational spectrum.

Now we substitute the $Y_J^m(\theta,\phi)$ into the equation and let $x=\cos\theta$ to obtain:

$$
\langle J’,m’|\mu_z|J,m \rangle =\mu_0N_{J’m’}N_{Jm} \int_0^{2\pi}d\phi e^{i(m-m’)\phi} \int_{-1}^{1} dx\ x P_{J’}^{|m’|}(x) P_J^{|m|}(x)
$$

The integral over $\phi$ is zero unless $m=m’$, so we find that $\Delta m=0$ is part of the rigid-rotator selection rule. Integration over $\phi$ for $m=m’$ gives a factor of $2\pi$, so we have:

$$
\langle J’,m’|\mu_z|J,m \rangle =2\pi\mu_0N_{J’m’}N_{Jm} \int_{-1}^{1} dx\ x P_{J’}^{|m’|}(x) P_J^{|m|}(x)
$$

We can evaluate this integral in general by using the recursion formula:

$$
(2J+1)xP_J^{|m|}(x)=(J-|m|+1)P_{J+1}^{|m|}(x)+(J+|m|)P_{J-1}^{|m|}(x)
$$

By using this relation, we obtain:

$$
\begin{aligned} \langle J’,m|\mu_z|J,m \rangle= &2\pi\mu_0N_{J’m}N_{Jm}\int_{-1}^1dx\ P_{J’}^{|m|}(x) \[3mm] &\times \left[\frac {(J-|m|+1)}{2J+1}P_{J+1}^{|m|}(x)+\frac {(J+|m|)}{2J+1}P_{J-1}^{|m|}(x) \right] \end{aligned}
$$

Using the orthogonality relation for the $P_J^m(x)$, we find that the above integral will vanish unless $J’=J+1$ or $J’=J-1$. This finding leads to the selection rule $J’=J\pm1$, or $\Delta J=\pm1$.

Thus, we have shown that the selection rule for pure rotational spectra in the rigid-rotator approximation is that the molecule must have a permanent dipole moment and that $\Delta J=\pm1$ and $\Delta m=0$.

（ 转动光谱的选律也和振动光谱类似，来自于递推关系的限制。 ）

6.8 The Precise Values of the Three Components of Angular Momentum Cannot Be Measured Simultaneously

Angular momentum plays a key role not only in the theory of the rigid rotator, but in the theory of the hydrogen atom as well. To keep things general, we’ll use $l$ for angular momentum and $m$ for its z component in this section.

Recall that angular momentum is a vector quantity. We can write the expression of the operator in spherical coordinates:

$$
\hat L_x=-i\hbar \left(-\sin\phi\frac {\partial}{\partial \theta}-cot\theta\ \cos\phi\frac {\partial}{\partial\phi} \right) \[3mm] \hat L_y=-i\hbar \left(\cos\phi\frac {\partial}{\partial \theta}-cot\theta\ \sin\phi\frac {\partial}{\partial\phi} \right) \[3mm] \hat L_z=-i\hbar\frac {\partial}{\partial\phi}
$$

We see that the spherical harmonics are eigenfunctions of $\hat L_z$:

$$
\begin{aligned} \hat L_zY_l^m(\theta,\phi) &=N_{lm}\hat L_zP_l^{|m|}(\cos\theta)e^{im\phi} \[3mm] &=N_{lm}P_l^{|m|}(\cos\theta)\hat L_ze^{im\phi} \[3mm] &= \hbar mY_l^m(\theta,\phi) \end{aligned}
$$

This equation shows that measured value of $L_z$ are integral multiples of $\hbar$.

However, the spherical harmonics are not eigenfunctions of $\hat L_x$ or $\hat L_y$.

Because the spherical harmonics are simultaneous eigenfunctions of both $\hat L^2$ and $\hat L_z$, we can determine precise values of $L^2$ and $L_z$ simultaneously (Section 4.4), which implies that the operators $\hat L^2$ and $\hat L_z$ commute.

We can prove that $|m| \le l$, or that $m=0,\pm1,\pm2,\cdots,\pm l$. It follows:

$$
(\hat L^2-\hat L_z^2)Y_l^m(\theta,\phi)=\hbar^2[l(l+1)-m^2]Y_l^m(\theta,\phi)
$$

Because:

$$
\hat L^2=\hat L_x^2+\hat L_y^2+\hat L_z^2
$$

then:

$$
(\hat L^2-\hat L_z^2)Y_l^m(\theta,\phi)=(\hat L_x^2+\hat L_y^2)Y_l^m(\theta,\phi)=\hbar^2[l(l+1)-m^2]Y_l^m(\theta,\phi)
$$

Thus, the observed values of $L_x^2+L_y^2$ are $[l(l+1)-m^2]\hbar^2$. But because $L_x^2+L_y^2$ is the sum of two squared terms, it cannot be negative, and so we have:

$$
[l(l+1)-m^2]\hbar^2 \ge 0
$$

or

$$
l(l+1) \ge m^2
$$

Because $l$ and $m$ are integers, so it says that:

$$
|m| \le l
$$

or that the only possible values of the integer $m$ are:

$$
m=0,\pm1,\pm2,\cdots,\pm l
$$

The equation shows that there are $2l+1$ values of $m$ for each value of $l$.

We can prove:

$$
[\hat L^2,\hat L_x]=[\hat L^2,\hat L_y]=[\hat L^2,\hat L_z]=0
$$

But they do not commute among themseles:

$$
\left[\hat L_x,\hat L_y \right] =i\hbar\hat L_z \[3mm] \left[\hat L_y,\hat L_z \right]=i\hbar\hat L_x \[3mm] \left[\hat L_z,\hat L_x \right]=i\hbar\hat L_y
$$

It is possible to observe precise values of $L^2$ and $L_z$ simultaneously, it is not possible to observe precise values of $L_x$ and $L_y$ simultaneously because they do not commute with each other.

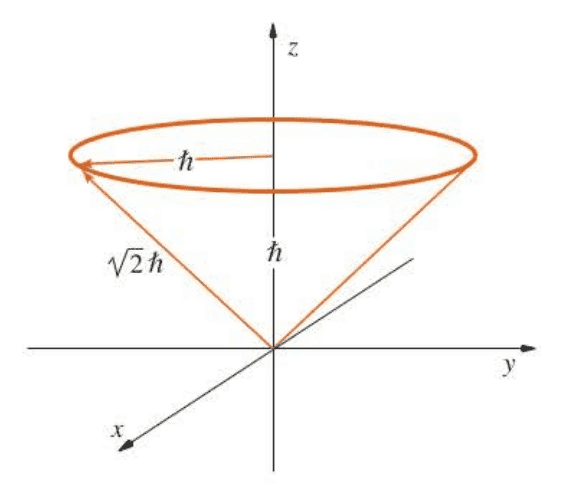
Even though $L_x$ and $L_y$ do not have precise values, they do have an average value:

$$
\langle L_x \rangle=\langle L_y \rangle =0
$$

A nice classical interpretation of these results is that $L$ precesses about the z axis, mapping out the surface of the cone shown there. The average values of $\langle L_x \rangle$ and $\langle L_y \rangle$ are zero. This picture is in nice accord with the uncertainty principle: by specifying $L_z$ exactly, we have a complete uncertainty in the angle $\phi$ associated with $L_z$.

Before leaving this section, we should address the following question: What is so special about the z direction? The answer is that nothing at all is special about the z direction. We could have chosen either the x or y direction as the unique direction and all the above results would be the same, except for exchanging x or y for z.

（ 角动量平方算符和角动量z轴分量算符对易，因此可以同时测得角动量大小和它在z轴分量的大小。但是在x-y平面的方向则无法确定，因为$\hat L_z$与$\hat L_x/\hat L_y$均不对易，所以它的图像很直观地对应于Figure 6.6中的圆锥图形。 ）

总结

本章讨论了刚性转子模型和转动光谱，总体思路实际上和上一章的振动光谱有很多相似。

本章章末附录中讨论了用算符方法计算角动量平方算符$\hat L^2$和角动量z轴分量算符$\hat L_z$的本征值关系的做法，同样是使用阶梯算符对球谐函数做处理，很自然就导出了$m$和$l$的关系，值得一看。