《Quantum Chemistry》章末总结5

第五章讲谐振子，这是量子力学的核心模型之一，同时学习振动光谱。

Chapter 5 The Harmonic Oscillator and Vibrational Spectroscopy

5.1 A Harmonic Oscillator Obeys Hooke’s Law

Consider a mass $m$ connected to a wall by a spring, as shown in Figure 5.1.

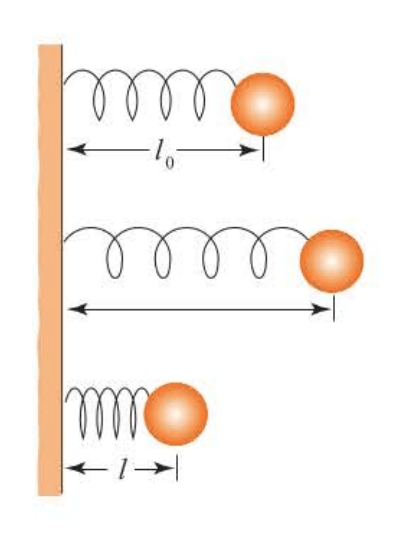
Suppose further that no gravitational force is acting on $m$ so that the only force is due to the spring.

If we let $l_0$ be the equilibrium, or undistorted, length of the spring, then the restoring force must be some function of the displacement of the spring from its equilibrium length. Let this displacement be denoted by $x=l-l_0$, where $l$ is the length of the spring. The simplest assumption we can make about the force on m as a function of the displacement is that the force is directly proportional to the displacement and to write:

$f=-k(l-l_0)=-kx$

The negative sign indicates that the force points to the right in Figure 5.1 if the spring is compressed ($l<l_0$) and points to the left ifthe spring is stretched ($l>l_0$). The equation is called Hooke’s law and the (positive) proportionality constant $k$ is called the force constant of the spring.

Newton’s equation with a Hooke’s law force is:

$m\frac {d^2l}{dt^2}=-k(l-l_0)$

If we let $x=l-l_0$, then we have:

$m\frac {d^2x}{dt^2}+kx=0$

The general solution to this equation is:

$x(t)=c_1sin\omega t+c_2cos\omega t$

where:

$\omega = \left(\frac km \right)^{1/2}$

Suppose we stretch the spring so that its displacement is A and then let go. The initial velocity is zero and we have:

$x(0)=c_2=A$

$\left(\frac {dx}{dt} \right)_{t=0}=0=c_1\omega$

And so:

$x(t)=Acos\omega t$

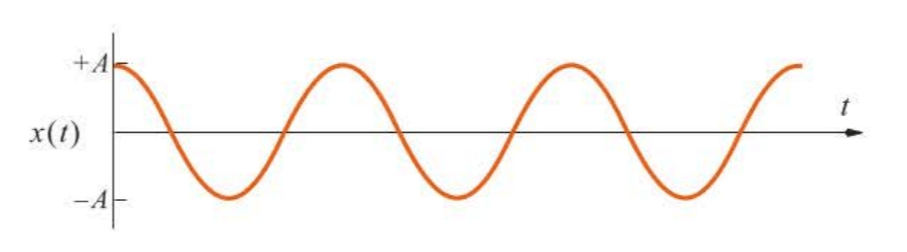
The displacement versus time is plotted in Figure 5.2, which shows that the mass oscillates back and forth between $A$ and $-A$ with a frequency $\omega$ radians per second, or $\nu=\omega/2\pi$ cycles per second. The quantity $A$ is called the amplitude of the vibration.

5.2 The Energy of a Harmonic Oscillator Is Conserved

Let’s look at the total energy of a harmonic oscillator. The potential energy is:

$V(x)=-\int f(x)dx+constant$

We can see that:

$V(x)=\frac {k}{2}x^2+constant$

The constant term here is an arbitrary constant that can be used to fix the zero of energy. If we choose the potential energy of the system to be zero when the spring is undistorted $(x=0)$, then we have:

$\begin{aligned} V(x) &=\frac k2x^2 \\[3mm] &=\frac 12kA^2cos^2\omega t \end{aligned}$

for the potential energy associated with a simple harmonic oscillator.

The kinetic energy is:

$\begin{aligned} T &=\frac 12m \left(\frac {dl}{dt} \right)^2=\frac 12m \left(\frac {dx}{dt} \right)^2 \\[3mm] &=\frac 12m\omega^2A^2sin^2\omega t \end{aligned}$

Both $T$ and $V$ are plotted in Figure 5.3. The total energy is:

$\begin{aligned} E=T+V &=\frac 12kA^2cos^2\omega t+\frac 12m\omega^2A^2sin^2\omega t \\[3mm] &=\frac 12kA^2 \end{aligned}$

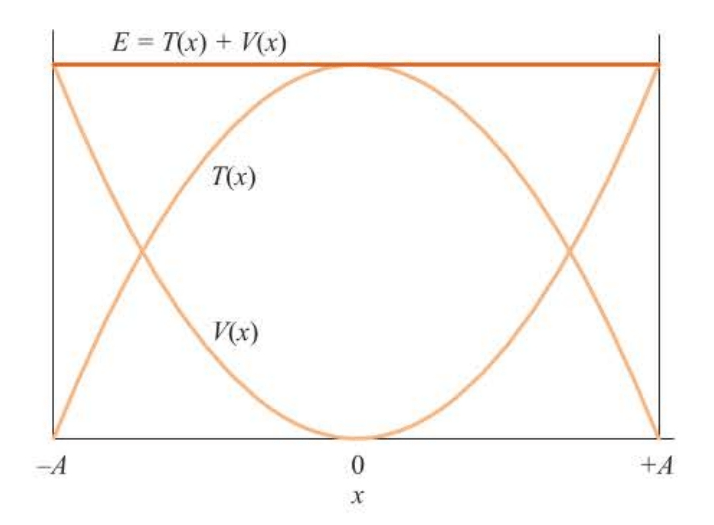
Thus, we see that the total energy is a constant and, in particular, is equal to the potential energy at its largest displacement, where the kinetic energy is zero.

Each oscillates between $+A$ and $-A$ but in such a way that their sum is always a constant. We say that the total energy is conserved and that the system is a conservative system.

（ 谐振子系统是一个保守系统，因为所受的弹簧弹力为保守力，系统的机械能（动能+势能）守恒。 ）

5.3 The Equation for a Harmonic-Oscillator Model of a Diatomic Molecule Contains the Reduced Mass of the Molecule

The simple harmonic oscillator is a good model for a vibrating diatomic molecule. A diatomic molecule, however, does not look like the system pictured in Figure 5.1, but more like two masses connected by a spring, as in Figure 5.4.

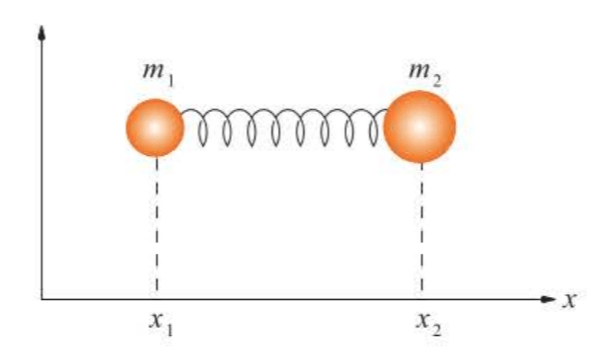
In this case we have two equations of motion, one for each mass:

$m_1\frac {d^2x_1}{dt^2}=k(x_2-x_1-l_0)$

$m_2\frac {d^2x_2}{dt^2}=-k(x_2-x_1-l_0)$

If we add the two equations, we find that:

$\frac {d^2}{dt^2}(m_1x_1+m_2x_2)=0$

This form suggests that we introduce a center-of-mass coordinate:

$X=\frac {m_1x_1+m_2x_2}{M} \quad (M=m_1+m_2)$

So:

$M\frac {d^2X}{dt^2}=0$

There is no force term here, so the equation shows that the center of mass moves uniformly in time with a constant momentum.

（ 从质心系角度出发的推导说明整个系统总体不受力的作用，系统总体的运动具有恒定的动量。 ）

The vibrational motion of the two-mass or two-body system in Figure 5.4 must depend upon only the relative separation of the two masses, or upon the relative coordinate.

$x=x_2-x_1-l_0$

If we rewrite the two equations of motion and use one subtract another:

$\begin{aligned} \frac {d^2x_2}{dt^2}-\frac {d^2x_1}{dt^2} &= -\frac {k}{m_2}(x_2-x_1-l_0)-\frac {k}{m_1}(x_2-x_1-l_0) \\[3mm] \frac {d^2}{dt^2}(x_2-x_1) &= -k \left(\frac 1{m_1}+\frac 1{m_2} \right)(x_2-x_1-l_0) \end{aligned}$

If we let:

$\frac 1{m_1}+\frac 1{m_2}=\frac {m_1+m_2}{m_1m_2}= \frac 1{\mu}$

and introduce $x=x_2-x_1-l_0$, then we have:

$\mu \frac {d^2x}{dt^2}+kx=0$

The quantity $\mu$, that we have defined is called the reduced mass.

Thus, the two-body system in Figure 5.4 can be treated as easily as the one-body problem in Figure 5. I by using the reduced mass of the two-body system.

（ 通过引入相对坐标系，我们利用折合质量/约化质量可以把一个两体问题转化为一个单体问题，这样双原子分子的振动就简化为了谐振子模型。 ）

5.4 The Harmonic-Oscillator Approximation Results from the Expansion of an Internuclear Potential Around lts Minimum

The internuclear potential for a diatomic molecule is illustrated by the solid line in Figure 5.5. The dashed line shows the potential associated with Hooke’s law.

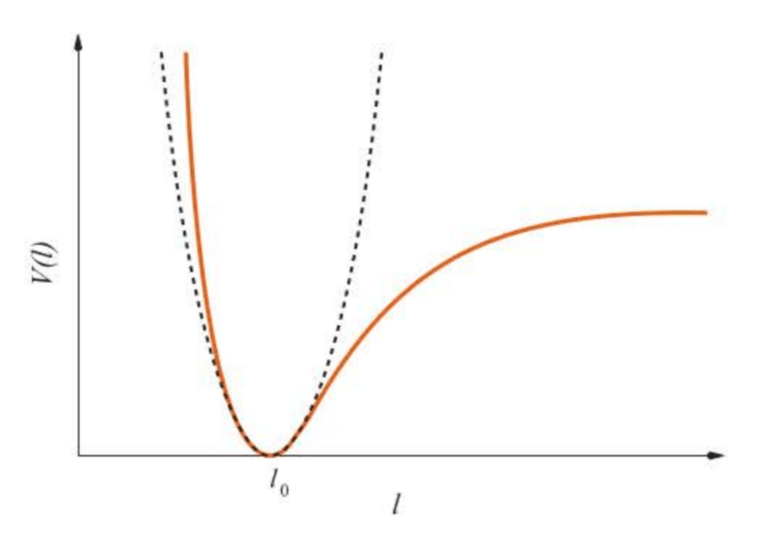
Although the harmonic-oscillator potential may appear to be a terrible approximation to the experimental curve, note that it is, indeed, a good approximation in the region of the minimum.

Although the harmonic oscillator unrealistically allows the displacement to vary from $-\infin$ to $+\infin$, these large displacements produce potential energies that are so large that they do not often occur in practice. The harmonic oscillator is a good approximation for vibrations with small amplitudes.

We consider the Taylor expansion of the potential energy $V(l)$ about the equilibrium bond length $l=l_0$. The first few terms in this expansion are:

$V(l)=V(l_0)+ \left(\frac {dV}{dl} \right)_{l=l_0}(l-l_0)+\frac {1}{2!} \left(\frac {d^2V}{dl^2} \right)_{l=l_0}(l-l_0)^2+\frac 1{3!} \left(\frac {d^3V}{dl^3} \right)_{l=l_0}(l-l_0)^3+\cdots$

Note that $dV/dl$ is the force acting between the two nuclei, and the fact that $dV/dl$ vanishes at $l=l_0$ means that the force acting between the nuclei is zero at this point. This is why $l=l_0$ is called the equilibrium bond length.

If we restrict ourselves to small displacements, then $l-l_0$ will be smal I and we can neglect the terms beyond the quadratic term in equation, showing that the general potential energy function $V(l)$ can be approximated by a harmonic-oscillator potential.

（ 谐振子在双原子分子势能最小值处是一个良好的近似模型。 ）

We can consider corrections or extensions of the harmonic-oscillator model by the higher-order terms. These are called anharmonic terms and will be considered in Section 5.7.

5.5 The Energy Levels of a Quantum-Mechanical Harmonic Oscillator Are $E_{\nu}=h\nu(\nu+\frac 12)$ with $\nu=0,1,2,\cdots$

The Schrödinger equation for a one-dimensional harmonic oscillator is:

$-\frac {\hbar^2}{2\mu}\frac {d^2\psi}{dx^2} + V(x)\psi(x)=E\psi(x)$

with $V(x)=\frac 12kx^2$. Thus, we must solve the second-order differential equation:

$\frac {d^2\psi}{dx^2}+\frac {2\mu}{\hbar^2} \left(E-\frac 12kx^2 \right)\psi(x)=0 \quad -\infin < x <\infin$

When a differential equation does not have constant coefficients, there is no simple, general technique for solving it. One method that often works, however laborious it is, is to substitute a power series into the differential equation and then determine each coefficient in the series sequentially.

（ 幂级数展开法对于这种层次的化学教材来说还是太难了点XD ）

When the equation is solved, well-behaved, finite solutions can be obtained only if the energy is restricted to the quantized values:

$E_{v}=h\nu(v+\frac 12) \quad v=0,1,2,\cdots$

where:

$\nu=\frac 1{2\pi} \left(\frac {k}{\mu} \right)^{1/2}$

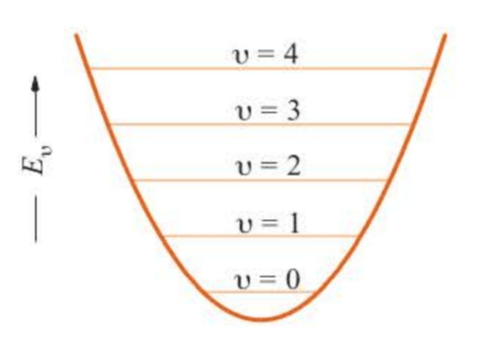
The energies are plotted in Figure 5.6. Note that the energy levels are equally spaced, with a separation $h\nu$.

Note also that the energy of the ground state, the state with $\nu=0$, is $\frac 12h\nu$ and is not zero as the lowest classical energy is. This energy is called the zero-point energy of the harmonic oscillator and is a direct result of the uncertainty principle.

The energy of a harmonic oscillator can be written in the form $(p^2/2\mu)+(kx^2/2)$, and so we see that a zero value for the energy would require that both $p$ and $x$ or, more precisely, the expectation values of $\hat P^2$ and $\hat X^2$ be simultaneously zero, in violation of the uncertainty principle.

（ 零点能来自于不确定原理，因为动量和位置无法同时确定，所以动能和势能无法同时为零。 ）

5.6 The Harmonic Oscillator Accounts for the Infrared Spectrum of a Diatomic Molecule

The vibrational energy levels of the diatomic molecule are given by:

$E_v=h\nu \left(v+\frac 12 \right)\quad v=0,1,2,\cdots$

A diatomic molecule can make a transition from one vibrational energy state to another by absorbing or emitting electromagnetic radiation whose observed frequency satisfies the Bohr frequency condition:

$\Delta E=h\nu_{obs}$

We will prove in Chapter 8 that the harmonic-oscillator model allows transitions only between adjacent energy states, so that we have the condition that $\Delta v=\pm1$. Such a condition is called a selection rule.

Thus, the observed frequency of the radiation absorbed is:

$\nu_{obs}=\frac 1{2\pi} \left(\frac {k}{\mu} \right)^{1/2}\ \ (Hz)$

So this model predicts that the spectrum consists of just one line. This
prediction is in good accord with experiment, and this line is called the fundamental vibrational frequency. For diatomic molecules, these lines occur at around $10^{14}$ Hz, which is in the infrared region.

It is customary in discussions of vibrational spectroscopy to write the vibrational energy level in the form:

$G(v)=\frac {E_v}{hc}=\tilde \omega \left(v+\frac 12 \right)$

$\tilde \omega=\frac 1{2\pi c} \left(\frac k{\mu} \right)^{1/2}\ \ (cm^{-1})$

$G(v)$ is called the vibrational term, and $\tilde \omega$ have units of $cm^{-1}$, called wave number.

5.7 Overtones Are Observed in Vibrational Spectra

The harmonic-oscillator approximation predicts that there will be only one line in the vibrational spectrum of a diatomic molecule. Expermental data show there is, indeed, one dominant line (the fundamental), but there are also lines of weaker intensity at almost integral multiples of the fundamental. These lines are called overtones.

Recall that the potential energy $V(l)$ may be expanded in a Taylor series about $l_0$, the value of $l$ at the minimum of $V(l)$, to give:

$\begin{aligned} V(l)-V(l_0) &=\frac 1{2!} \left(\frac {d^2V}{dl^2} \right)_{l=l_0}(l-l_0)^2 +\frac 1{3!} \left(\frac {d^3V}{dl^3} \right)_{l=l_0}(l-l_0)^3 + \cdots \\[3mm] &= \frac k2x^2+\frac {\gamma_3}6x^3 + \frac {\gamma_4}{24}x^4+\cdots \end{aligned}$

lf the anharmonic terms in equation are included in the Hamiltonian operator for the vibrational motion of a diatomic molecule, the Schrödinger equation can be solved by a technique called perturbation theory to give:

$G(v)=\tilde \omega_e \left(v+\frac 12 \right)-\tilde x_e\tilde \omega_e \left(v+\frac 12 \right)^2+\cdots \quad v=0,1,2,\cdots$

where $\tilde x_e$ is called the anhannonicity constant. The anharmonic correction is much smaller than the harmonic term because $\tilde x_e \ll1$.

Figures 5.7 and 5.8 show the levels given by the equation. Notice that the levels are not equally spaced as they are for a harmonic oscillator and, in fact, that their separation decreases with increasing $\nu$.

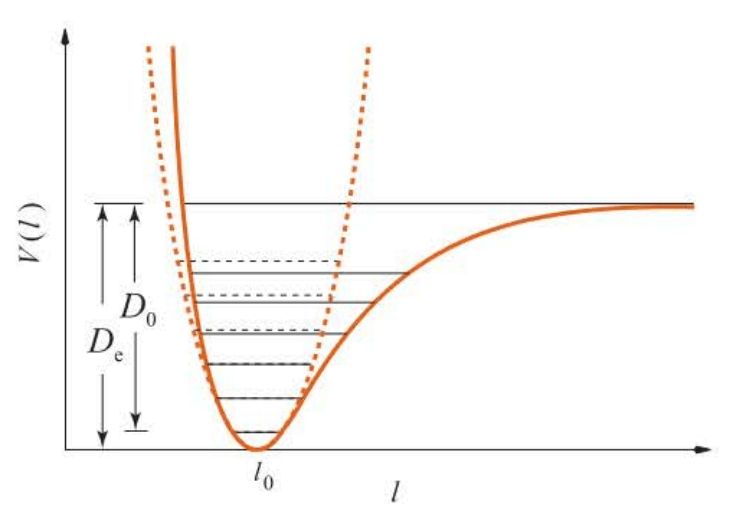
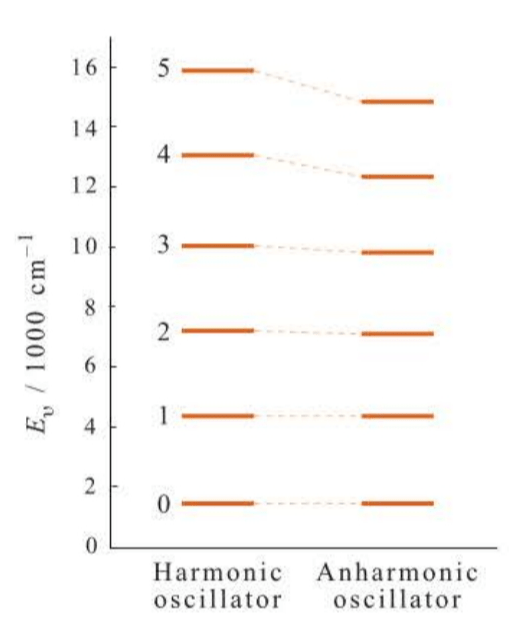
Figure 5.7 also shows two quantities $D_e$ and $D_0$. The energy difference between the minimum of the potential well at the dissociation limit is $D_e$; the energy difference between the zero-point vibrational energy and the dissociation limit is $D_0$. They are related by:

$D_0=D_e-\frac 12h\nu$

It’s $D_0$ that is measured experimentally.

The selection rule for an anharmonic oscillator is that $\Delta \nu$ can have any integral value, although the intensities of the $\Delta\nu=\pm2,\pm3,\cdots$ transitions are much less than for the $\Delta\nu=\pm1$ transitions.

5.8 The Harmonic-Oscillator Wave Functions Involve Hermile Polynomials

The wave functions corresponding to the $E_v$ for a harmonic oscillator are nondegenerate and are given by:

$|v\rangle=N_vH_v(\alpha^{1/2}x)e^{-\alpha x^2/2}$

where:

$\alpha= \left(\frac {k\mu}{\hbar^2} \right)^{1/2}$

$N_v=\frac 1{(2^v)v!} \left(\frac {\alpha}{\pi} \right)^{1/4}$

and the $H_v(\alpha^{1/2}x)$ are polynomials called Hermite polynomials. Note that $H_v(\xi)$ is a $v$th-degree polynomial in $\xi$.

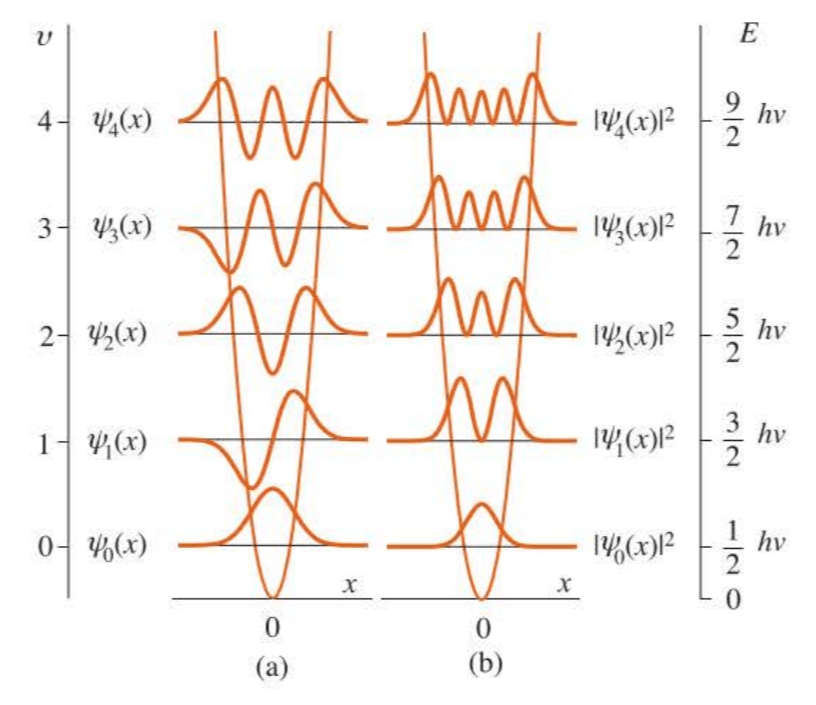
We can show explicitly that the $\psi_v(x)$ are normalized, or that $N_v$ is the normalization constant. And we say that the Hermite polynomials are orthogonal with respect to the weighting function $e^{-\xi^2}$.

5.9 Hermite Polynomials Are Either Even or Odd Functions

The harmonic-oscillator wave functions are:

$|v\rangle=N_vh_v(\alpha^{1/2}x)e^{-\alpha x^2/2}$

The $\psi_v(x)$ are even when $v$ is an even integer and odd when $v$ is an odd integer. So $\psi_v^2(x)$ is an even function for any value of $v$. Then:

$\langle x \rangle = \langle v|x|v \rangle =0$

Beceuse the integrand is an odd function for any value of $v$. Thus, the average displacement of a harmonic oscillator is zero for all the quantum states of a harmonic oscillator, or the average internuclear separation is the equilibrium bond length $l_0$.

The average momentum is given by:

$\langle p \rangle=\langle v|\hat P_x|v \rangle = \int_{-\infin}^{\infin}\psi_v(x) \left(-i\hbar\frac {d}{dx} \right)\psi_v(x)dx=0$

The derivative of an odd (even) function is even (odd), so this integral vanishes because the integrand is the product of an odd and even function and hence is overall odd. Thus, $\langle p \rangle =0$ for a harmonic operator.

（ 厄米多项式的奇偶性从推导过程中更易于发现，这里只给出结论。这种对称性通常运用在运算过程中以简化计算。 ）

5.10 There Are Many Useful Relations Among Hermite Polynomials

There are a number of relations involving the Hermite polynomials that can be used to evaluate integrals. A particularly useful one is:

$H_{v+1}(\xi) - 2\xi H_v(\xi) + 2vH_{v-1}(\xi)=0$

This is a recursion formula for the $H_v(\xi)$.

Recursion formulas can be used to evaluate integrals involving Hermite polynomials. For example:

$\langle \xi^2 \rangle =N_v^2\int_{-\infin}^{\infin}d\xi H_v(\xi)\xi^2H_v(\xi)e^{-\xi^2}$

Apply the recursion formula and rewrite the expression:

$\begin{aligned} \xi^2H_v(\xi) &=v \left[(v-1)H_{v-2}(\xi)+\frac 12H_v(\xi)\right]+\frac 12 \left[(v+1)H_v(\xi)+\frac 12H_{v+2}(\xi)\right] \\[3mm] &=v(v-1)H_{v-2}(\xi)+(v+\frac 12)H_v(\xi)+\frac 14H_{v+2}(\xi) \end{aligned}$

When we substitute this into the equation, we obtain:

$\begin{aligned} \langle \xi^2 \rangle &=\langle v|\xi^2|v \rangle \\[3mm] &= N_v^2\int_{-\infin}^{\infin}d\xi H_v(\xi) \left[v(v-1)H_{v-2}(\xi)+(v+\frac 12)H_v(\xi)+\frac 14H_{v+2}(\xi)\right] \\[3mm] &= \left(v+\frac 12 \right)N_v^2\int_{-\infin}^{\infin}d\xi H_v(\xi)H_v(\xi)e^{-\xi^2} \\[3mm] &=v + \frac 12 \end{aligned}$

Because $\xi=\alpha^{1/2}x$, we have:

$\langle x^2 \rangle = \frac 1{\alpha}\langle \xi^2 \rangle=\frac 1{\alpha} \left(v+\frac 12 \right)=\frac {\hbar}{(\mu k)^{1/2}} \left(v+\frac 12 \right)$

5.11 The Vibrations of Polyatomic Molecules Are Represented by Normal Coordinates

The vibrational spectra of polyatomic molecules turn out to be easily understood in the harmonic-oscillator approximation. The key point is the introduction of normal coordinates, which we discuss in this section.

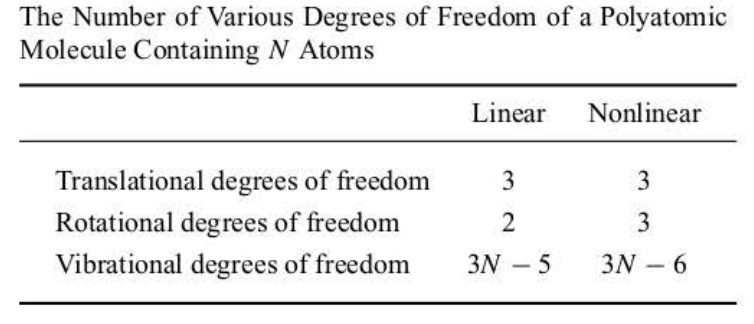
Consider a molecule containing N nuclei. A complete specification of this molecule in space requires 3N coordinates, three cartesian coordinates for each nucleus. We say that the N-atomic molecule has a total of 3N degrees of freedom.

Of these 3N coordinates, three can be used to specify the center of mass of the molecule. Motion along these three coordinates corresponds to translational motion of the center of mass of the molecule, and so we call these three coordinates translational degrees of freedom.

（ 平动自由度是由质心的运动决定的。 ）

It requires two coordinates to specify the orientation of a linear molecule about its center of mass and three coordinates to specify the orientation of a nonlinear molecule about its center of mass. Because motion along these coordinates corresponds to rotational motion, we say that a linear molecule has two degrees of rotational freedom and that a nonlinear molecule has three degrees of rotational freedom.

（ 空间中的转动可以用欧拉角来描述，用Pitch-Yaw-Roll三个角度就可以描述任何转动。对于线性双原子分子来说，由于分子键轴是$C_{\infin}$轴，所以不需要Roll角，只需要其他两个角度就可以描述其转动，因此是两个转动自由度。 ）

The remaining coordinates (3N-5 for a linear molecule and 3N-6 for a nonlinear molecule) specify the relative positions of the N nuclei. Because motion along these coordinates corresponds to vibrational motion, we say that a linear molecule has 3N-5 vibrational degrees of freedom and that a nonlinear molecule has 3N-6 vibrational degrees of freedom.

（ 总自由度减去平动和转动，剩下的就是振动自由度了。 ）

In the absence of external fields, the energy of a molecule does not depend upon the position of its center of mass or its orientation. The potential energy of a polyatomic molecule is therefore a function of only the 3N-5 or 3N-6 vibrational coordinates.

If we let the displacements about the equilibrium values of these coordinates be denoted by $x_1,x_2,\cdots,x_{N_{vib}}$ where $N_{vib}$ is the number of vibrational degrees of freedom, then the potential energy is given by:

$\begin{aligned} \Delta V &=V(x_1,x_2,\cdots,x_{N_{vib}})-V(0,0,\cdots,0) \\[3mm] &=\frac 12\sum_{i=1}^{N_{vib}}\sum_{j=1}^{N_{vib}} \left(\frac {\partial^2V}{\partial x_i\partial x_j} \right)x_ix_j+\cdots \\[3mm] &=\frac 12\sum_{i=1}^{N_{vib}}\sum_{j=1}^{N_{vib}}f_{ij}x_ix_j+\cdots \end{aligned}$

In general, there are other terms that contain higher powers of $x_i$, but these anharmonic terms are neglected here.

The presence of the cross terms in the equation makes the solution of the corresponding Schrödinger equation very difficult to obtain. A theorem of classical mechanics, however, allows us to eliminate all the cross terms. A straightforward procedure using matrix algebra can be used to find a new set of coordinates {$Q_j$}, such that:

$\Delta V=\frac 12\sum_{j=1}^{N_{vib}}F_jQ_j^2$

These new coordinates are called normal coordinates or normal modes. In terms of normal coordinates, the vibrational Hamiltonian operator is:

$\hat H_{vib}=-\sum_{j=1}^{N_{vib}}\frac {\hbar^2}{2\mu_j}\frac {d^2}{dQ_j^2}+\frac 12\sum_{j=1}^{N_{vib}}F_jQ_j^2$

Recall from Section 3.9 that if a Hamiltonian operator can be written as a sum of independent terms, the total wave function is a product of individual wave functions and the energy is a sum of independent energies:

$\hat H_{vib}=\sum_{j=1}^{N_{vib}}\hat H_{vib,j}=\sum_{j=1}^{N_{vib}} \left(-\frac {\hbar^2}{2\mu_j}\frac {d^2}{dQ_j^2}+\frac 12F_jQ_j^2 \right) \\[3mm] \psi_{vib}(Q_1,Q_2,\cdots,Q_{vib})=\psi_{vib,1}(Q_1)\psi_{vib,2}(Q_2)\cdots\psi_{vib,N_{vib}}(Q_{N_{vib}})$

and:

$E_{vib}=\sum_{j=1}^{N_{vib}}h\nu_j \left(\nu_j+\frac 12 \right) \quad each\ \nu_j=0,1,2,\cdots$

（ 哈密顿量可以写成几个独立组分的哈密顿量的加和，而总波函数可以写成几个独立组分波函数的乘积。结果是，总能量为各独立部分的能量之和，见3.9节。

一般形式下的哈密顿量的势能项是耦合的，这使得求解薛定谔方程变得非常困难。引入简正坐标的目的就是为了消去交叉项，即“解耦”。分离变量后，方程就变成了多个谐振子方程，分子总的振动可以看作多个简正模的叠加。 ）

5.12 The Harmonic-Oscillator Selection Rule Is $\Delta v=\pm1$

In this section, we shall discuss a selection rule. We shall show in Section 8.6 that if a harmonic oscillator is irradiated with electromagnetic radiation propagating in the z direction, then the probability that the oscillator makes a transition from state $v$ to state $v'$ is proportional to the square of the integral:

$\langle v|\mu_z|v' \rangle =\int_{-\infin}^{\infin}dx \psi_v(x)\mu_z(x)\psi_{v'}(x)$

where $\mu_z$ is the z component of the dipole moment. This type of integral, which occurs frequently in spectroscopy, is called a dipole transition moment.

We now expand $\mu_z(x)$ about the equilibrium nuclear separation:

$\mu_z(x)=\mu_0+ \left(\frac {d\mu}{dx}\right)_0x+\cdots$

where $\mu_0$ is the dipole moment at the equilibrium bond length and $x$ is the displacement from that equilibrium value. Thus, when $x=0,\mu_z=\mu_0$. We substitute the equation into the expression of dipole transition moment:

$\langle v|\mu_z|v' \rangle = \mu_0\langle v|v' \rangle + \left(\frac {d\mu}{dx}\right)_0 \langle v|x|v' \rangle$

The first integral here vanishes if $v\ne v'$ due to the orthogonality of the harmonic-oscillator wave functions. The second integral can be evaluated in general by using:

$\xi H_v(\xi)=vH_{v-1}(\xi)+\frac 12H_{v+1}(\xi) \quad (\xi=\alpha^{1/2}x)$

so we obtain:

$\langle v|\mu_z|v' \rangle = \frac {N_vN_{v'}}{\alpha} \left(\frac {d\mu}{d\xi}\right)_0 \int_{-\infin}^{\infin}H_{v'}(\xi) \left[vH_{v-1}(\xi)+\frac 12H_{v+1}(\xi) \right]e^{-\xi^2}d\xi$

Using now the orthogonality property of the Hermite polynomials, we see that $\langle v|\mu_z|v' \rangle$ vanishes unless $v'=v\pm1$. Thus, the selection rule for vibrational transitions under the harmonic-oscillator approximation is that $\Delta v=\pm1$.

（ 我们可以发现选律的产生实际上是因为厄米多项式的递推公式的限制。 ）

In addition, the factor $(d\mu/d\xi)_0$ in front of the transition moment integral reminds us that the dipole moment of the molecule must vary during a vibration, or the transition will not take place.

A selection rule for vibrational absorption spectroscopy is that the dipole moment of the molecule must vary during the normal mode motion. When this is so, the normal mode is said to be infrared active. Otherwise, it is infrared inactive.

The normal modes of $H_2O$ are as follows:

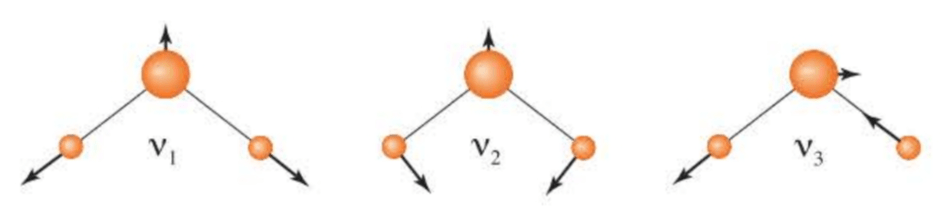
Note that the dipole moment changes during the motion of all three normal modes, so all three normal modes of $H_2O$ are infrared active. Therefore, $H_2O$ has three bands in its infrared spectrum.

（ 简正模的偶极矩发生变化才会产生跃迁偶极矩，即具有红外活性，才会在红外光谱上显示谱线。 ）

总结

本章最后的附录中介绍了代数法解决谐振子的薛定谔方程，构造升/降阶算符来求解波函数。在此处略去。

从这章开始，随着量子力学基本模型和光谱的引入，内容难度也比之前高了不少，具体的数理计算过程可以暂时放下，不过如果能结合计算过程来思考，很多东西的来龙去脉就会更清晰可见。