《物理化学》章末总结2

第二章进入热力学部分，参考教材是南大物化第二章和Atkins第二章。

第二章 热力学第一定律

2.1 热力学概论

热力学（thermodynamics）研究宏观系统的热现象、热和其他形式能量之间的转换关系，以及系统变化时所引起的这些物理量的变化。运用热力学中的基本原理研究化学现象以及和化学有关的物理现象，称为化学热力学（chemical thermodynamics）。

化学热力学的主要内容是根据热力学第一定律来计算变化中的热效应，根据热力学第二定律来解决变化的方向和限度问题，以及相平衡和化学平衡中的有关问题。热力学第三定律是一个关于低温现象的定律，主要阐明了规定熵的数值。有了这个定律，在原则上，只要利用热化学的有关数据就能解决有关化学平衡的计算问题。热力学第零定律则是热平衡的互通性，并为温度建立了严格的科学定义。

热力学的研究对象是大数量分子的集合体，因此所得到的结论具有统计学意义，只反映它的平均行为，而不适用于个别分子的个体行为。热力学方法的特点是不考虑物质的微观结构和反应进行的机理。

2.2 热平衡和热力学第零定律——温度的概念

如果两个系统分别和处于确定状态的第三个系统达到热平衡，则这两个系统彼此也将处于热平衡。这个平衡的规律称为热力学第零定律（zeroth law of thermodynamics）。这个结论是大量实验事实的总结和概括，它不能由其他的定律或定义导出。

通过这一定律，可以导出温度的科学定义，当两个系统接触并达到平衡，意味着这两个系统必定有一个共同的物理性质，这个物理性质就表述为“温度”。详细的推导见2.17节。

2.3 热力学的一些基本概念

此部分主要涉及一些基础概念的介绍，简要摘取部分重点。

系统与环境：

• 隔离系统/孤立系统（isolated system），系统与环境没有物质或能量的交换。
• 封闭系统（closed system），系统与环境没有物质交换，但可以发生能量交换。
• 敞开系统（open system），系统与环境既有物质交换，又有能量交换。

系统的性质：

• 广度性质（extensive property），其数值与系统的数量成正比，如体积、质量、熵、热力学能等。
• 强度性质（intensive property），其数值不具有加和性，取决于系统自身特性，与系统数量无关，如温度、压力、密度等。

热力学平衡态：

• 热平衡（thermal equilibrium），系统各部分温度相等。
• 力学平衡（mechanical equilibrium），系统各部分没有不平衡的力存在。
• 相平衡（phase equilibrium），系统物质在各相之间的分布达到平衡。
• 化学平衡（chemical equilibrium），系统的组成不再（通过化学反应）改变。

状态函数与状态方程：

• 用以描述系统状态的参数叫状态参数（state parameter），只与系统的状态有关的参数称为状态函数（state function）。相应的，如果会被状态改变的途径影响的参数称为途径/过程函数。状态函数在数学上具有全微分的性质，可以按照全微分的关系来处理。
  （ 对状态函数全微分在下文的推导过程中多次应用，Atkins甚至还专门讨论了与之相关的精确/不精确积分问题。 ）
• 系统状态函数之间的定量关系式称为状态方程（equation of state）。

过程和途径：

系统由始态到终态的变化，发生了一个热力学过程，，简称过程（process）。而一个过程可以经由多种不同的途径（path）实现。

• 等温过程（isothermal process）、等压过程（isobaric process）、等容过程（isochoric process）都很好理解。
• 绝热过程（adiabatic process），系统在变化过程中与环境没有热交换，或是变化太快来不及发生热交换。
• 环状过程（cyclic process），或称循环过程，系统从始态出发，经过一系列变化又回到原来状态。

热和功：

• 热力学研究的方法是宏观的，其给热（heat）下的定义是，由于温度不同而在系统与环境间交换或传递的能量。规定当系统吸热，$Q$取正值；系统放热，$Q$取负值。
• 热力学中除了热以外其他以其他形式传递的能量称为功（work），系统对外做功，$W$取负值；环境对系统做功，$W$取正值。

（ 热力学从宏观角度给出的定义还是挺“草率”的，但是在2.16节有微观上的数学解释。在此先摘取一段Atkins上的微观解释。

When energy is transferred to the surroundings as heat, the transfer stimulates random motion of the atoms in the surroundings. Transfer of energy from the surroundings to the system makes use of random motion (thermal motion) in the surroundings.

When a system does work, it stimulates orderly motion in the surroundings. For instance, the atoms shown here may be part of a weight that is being raised. The ordered motion of the atoms in a falling weight does work on the system.

…

In molecular terms, work is the transfer of energy that makes use of organized motion of atoms in the surroundings and heat is the transfer of energy that makes use of their disorderly motion.

微观层面上，功可以看作是使分子定向移动的能量，而热是让分子发生无序热运动的能量。这种“有序”和“无序”的对比也能够从2.16节的数学推导中体会出。

）

2.4 热力学第一定律

热力学能（thermodynamics energy）是值系统内分子运动的平动能、转动能、振动能、电子及核的能量，也称为内能（internal energy）。化学热力学中通常研究宏观静止的系统，而且一般没有特殊外力场存在，所以一般只注意热力学能。

热力学第一定律（first law of thermodynamics）的数学表达形式是：

$$
\Delta U = Q + W
$$

热力学第一定律说明了热力学能、热和功可以互相转换，体现了能量守恒的思想。热力学第一定律是人类经验的总结。

根据热力学第一定律，想制造一种机器，它既不考外界供给能量，本身也不减少能量，却能不断地对外工作，这是不可能的，也就是说，第一类永动机（first kind of perpetual motion machine）不可能制成。

热力学能是状态函数，所以决定热力学能的变量和决定系统状态的变量一样多，经验证明，从$p,V,T$中任选两个独立参数，再加上物质的量$n$，就可以决定系统状态。

2.5 准静态过程与可逆过程

热力学能只由状态决定，而功却与变化的具体途径有关。

考察气体的膨胀过程，设在定温下，将定量气体置于一个不计摩擦，横截面积为$A$的活塞筒中，忽略活塞质量。由于系统膨胀时要对抗外压做功，所以活塞移动$dl$时，系统做的膨胀功可以表示为：

$$
\delta W= -F_edl = -\left(\frac {F_e}A \right)\left(Adl \right) = -p_edV
$$

从状态1（$p_1,V_1,T_1$）到状态2（$p_2,V_2,T_2$）的过程，可以有许多途径，不同途径做功的数值不同，所以功与变化途径有关，也即功为途径函数。

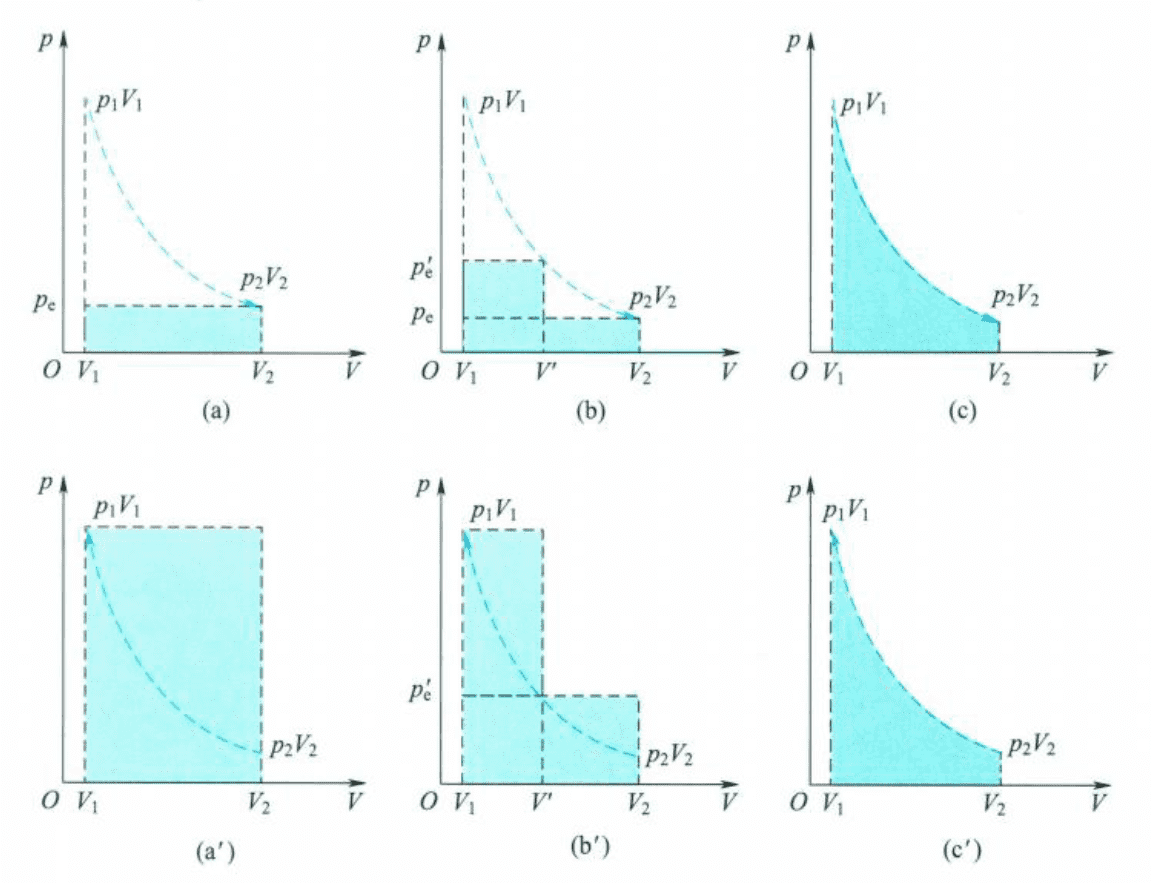
上图中（c）是膨胀过程中膨胀功最大的途径，此过程可以看作是无限多次等压膨胀，每次膨胀的外压都比内压差出一个无穷小，活塞的移动也非常慢，慢到以零为极限，这样就有足够的时间使气体的压力由微小的不均匀变为均匀。

整个过程可以看成由一系列接近于平衡的状态所构成，这种过程称为准静态过程（quasistatic process）。

类似的图2.1（c’）则是压缩过程的准静态过程。不难得出，在膨胀过程中的准静态过程做最大功，在压缩过程中的准静态过程做最小功，最大功和最小功数值相等，符号相反。

某一系统发生状态的改变后，如果系统经过某一过程重新回到了初始的状态且环境也完全复原，则这样的过程称为可逆过程（reversible process），反之称为不可逆过程（irreversible process）。上文提到的准静态过程在没有任何耗散的情况下就是一种可逆过程。

在可逆膨胀过程中系统做的功最大，而使系统复原的可逆压缩过程中环境做功最小，这样的两个过程的结合使系统和环境都完全恢复，称为可逆循环过程（reversible cyclic process）。

注意不可逆过程不是不能复原的过程，而是如果系统恢复，环境会发生某些变化（如环境失去功而获得了热，热功交换的不可逆性）。从消耗及获得能量的观点看，可逆过程是效率最高的过程，是提高实际过程效率的最高限度。

（ 可逆过程可以以最小的输入得到最大的输出，所以说它是效率最高的过程，当然实际情况中不可能达到这种效率，因为有各种损耗。而且可逆过程是一个时间无限长的过程，实际肯定要考虑时间因素。

可逆过程往往与平衡相联系。

A reversible change in thermodynamics is a change that can be reversed by an infinitesimal modification of a variable. The key word ‘infinitesimal’ sharpens the everyday meaning of the word ‘reversible’ as something that can change direction.

…

There is obviously a very close relationship between reversibility and equilibrium: systems at equilibrium are poised to undergo reversible change.

）

2.6 焓

热力学上给出焓（enthalpy）的定义，用符号$H$表示：

$$
H = U + pV
$$

数学推导

$U,p,V$都是由状态决定的，那么它们定义的焓也是状态函数，由于我们不能确定热力学能的绝对值，因此也无法确定焓的绝对值。

焓是认为定义的物理量，没有确切的意义，但是它在实用中很重要。没有其他功的条件下，系统在等容过程中所吸收的热全部用于增加热力学能；系统在等压过程中所吸收的热全部用于增加焓。

（ 人为定义了一个焓，其主要目的就是为了方便。等容条件下，系统的吸放热与热力学能的变化相联系。但是在等压过程中，系统吸放热没有直接相关的物理量，所以定义了一个焓，可以更简单的考虑问题。 ）

2.7 热容

对于没有相变和化学变化且不做非膨胀功的均相封闭系统，热容（heat capacity）的定义是系统升高单位热力学温度时所吸收的热，用符号$C$表示：

$$
C(T) = \frac {\delta Q} {dT}
$$

热容是广度量，而摩尔热容则是强度量：

$$
C_m(T) = \frac {C(T)} n = \frac {\delta Q} {ndT}
$$

等压过程的热容称为定压热容，用$C_p$表示；等容过程的热容称为定容热容，用$C_v$表示：

$$
C_p(T) = \frac {\delta Q_p} {dT} = \left(\frac {\partial H} {\partial T} \right)_p \quad \Delta H=Q_p = \int C_pdT
$$

$$
C_V(T) = \frac {\delta Q_V} {dT} = \left(\frac {\partial U} {\partial T} \right)_V \quad \Delta U=Q_V = \int C_VdT
$$

热容是温度的函数，这种函数关系因物质、物态、温度的不同而异。根据实验事实，常将气体的摩尔定压热容写成级数展开的经验形式。

（ 虽然热容是温度的函数，但是在变化幅度不大的情况下，经常把它当成常数计算。

The variation of heat capacity with temperature can sometimes be ignored if the temperature range is small; this is an excellent approximation for a monatomic perfect gas (for instance, one of the noble gases at low pressure). However, when it is necessary to take the variation into account for other substances.

）

2.8 热力学第一定律对理想气体的应用

上文提到过热力学能由$p,V,T$中任意两个独立变量来确定，因此推导出理想气体的热力学能仅是温度的函数，而与体积、压力无关，即：

$$
U=U(T)
$$

气体的热力学能是分子的动能和分子间相互作用的势能之和，而理想气体忽略了分子间作用力，所以理想气体的热力学能只考虑分子动能，因此只与温度有关，与体积无关。上式称为Joule定律。

对于这一结论，有Gay-Lussac - Joule实验加以验证：

很容易证明，理想气体的焓也仅为温度的函数：

$$
H=H(T)
$$

所以又得到，理想气体的$C_v$和$C_p$也是温度的函数。

在等容过程中，系统不做膨胀功，当升高温度时，它从环境所吸收的热全部用来增加热力学能。但在等压过程中，升高温度时，系统除增加热力学能外，还要多吸收一部分热以对外做功。因此对于气体来说，$C_p$恒大于$C_v$。

通过推导能够得到理想气体的$C_p$和$C_v$的关系：

$$
C_p - C_V = nR \quad C_{p,m} - C_{V,m} = R
$$

（ 南大书上这里的推导直接用数学方法处理，简单明了又很“暴力”。Atkins则是通过对物理过程的分析完成的，同时还引出了其他物理参数，也很有参考意义。此处两种方法都给出，以供对照。 ）

数学推导

南大教材：

对任意系统，有：

$$
\begin{equation}
\begin{align}
C_p - C_V =& \left(\frac {\partial H}{\partial T} \right)_p - \left(\frac {\partial U}{\partial T} \right)_V \nonumber \[3mm]
=& \left[\frac {\partial (U+pV)}{\partial T} \right]_p - \left(\frac {\partial U}{\partial T} \right)_V \nonumber \[3mm]
=& \left(\frac {\partial U}{\partial T} \right)_p + p\left(\frac {\partial V}{\partial T} \right)_p - \left(\frac {\partial U}{\partial T} \right)_V \nonumber
\end{align}
\end{equation}
$$

根据复合函数的偏微商公式：

$$
\left(\frac {\partial U}{\partial T} \right)_p = \left(\frac {\partial U}{\partial T} \right)_V + \left(\frac {\partial U}{\partial V} \right)_T \left(\frac {\partial V}{\partial T} \right)_p
$$

得：

$$
C_p - C_V = \left(\frac {\partial U}{\partial V} \right)_T\left(\frac {\partial V}{\partial T} \right)_p + p\left(\frac {\partial V}{\partial T} \right)_p = \left[p+\left(\frac {\partial U}{\partial V} \right)_T \right]\left(\frac {\partial V}{\partial T} \right)_p
$$

对于理想气体：

$$
\left(\frac {\partial U}{\partial V} \right)_T = 0 \quad \left(\frac {\partial V}{\partial T} \right)_p = \frac {nR}p
$$

带入上式，则得：

$$
C_p - C_V = nR
$$

---

Atkins:

首先是介绍了一下精确微分和不精确微分的概念，也就是说热力学能作为状态函数，它的值仅与状态有关，因此对热力学能的微分是精确微分，也就是满足全微分条件。

$$
dU = \left(\frac {\partial U}{\partial V} \right)_TdV + \left(\frac {\partial U}{\partial T} \right)_V dT
$$

然后引入了内压力（internal pressure）$\pi _T$的概念，将上式变形：

$$
dU = \pi _TdV + C_VdT
$$

The other coefficient, denoted $\pi _T$ plays a major role in thermodynamics because it is a measure of the variation of the internal energy of a substance as its volume is changed at constant temperature. Because $\pi _T$ has the same dimensions as pressure but arises from the interactions between the molecules within the sample, it is called the internal pressure.

右侧第一项的系数即为内压力，它反映的是恒定温度下内能随体积变化产生的变化。

在等压条件下，将上式继续变形，左右两侧同除$dT$：

$$
\left(\frac {\partial U}{\partial T} \right)_p = \pi _T \left(\frac {\partial V}{\partial T} \right)_p + C_V
$$

继续从该式中发掘物理意义，右侧的$\left(\frac {\partial V}{\partial T} \right)_p$描述了恒定压强下体积随温度的变化而变化的程度，换句话说，描述了气体在温度改变时是否易于压缩/膨胀，因此引入膨胀系数（expansion coefficient）$\alpha$：

$$
\alpha = \frac 1 V \left(\frac {\partial V}{\partial T} \right)_p
$$

As already emphasized, it is usually sensible in thermodynamics to inspect the output of a manipulation to see if it contains any recognizable physical quantity. The partial derivative on the right in this expression is the slope of the plot of volume against temperature (at constant pressure). This property is normally tabulated as the expansion coefficient.

因此上式可变形为：

$$
\left(\frac {\partial U}{\partial T} \right)_p = \alpha \pi _T V +C_V
$$

对于理想气体来说，忽略其分子间的作用力，因此内压力$\pi _T =0$，所以得到：

$$
C_V = \left(\frac {\partial U}{\partial T} \right)_p
$$

注意上式与定义式不同，等容热容的定义是恒定体积下，内能对温度的偏导。而上式是恒定压强下内能对温度的偏导，该式仅对于理想气体才成立。

That is, although the constant-volume heat capacity of a perfect gas is defined as the slope of a plot of internal energy against temperature at constant volume, for a perfect gas CV is also the slope of a plot of internal energy against temperature at constant pressure.

算了一大圈得到了这个式子，但是这个表达式对于计算$C_p$与$C_V$的差很有帮助：

$$
\begin{equation}
\begin{align}
C_p - C_V =& \left(\frac {\partial H}{\partial T} \right)_p - \left(\frac {\partial U}{\partial T} \right)_p \nonumber \[3mm]
=& \left[\frac {\partial (U+pV)}{\partial T} \right]_p - \left(\frac {\partial U}{\partial T} \right)_p \nonumber \[3mm]
=& \left[\frac {\partial (U+nRT)}{\partial T} \right]_p - \left(\frac {\partial U}{\partial T} \right)_p = nR \nonumber
\end{align}
\end{equation}
$$

统一了角标之后的计算就很容易了。Atkins的方法的巧妙之处就是他很好地为式子赋予了物理意义，再加以合理的变形转化，推导出新的结论。

在绝热系统中发生的过程称为绝热过程（adiabatic process）。气体若在绝热情况下膨胀，由于不能从环境吸取热，对外做功所消耗的能量不能从外界得到补偿，只能降低自身的热力学能，于是系统的温度必然有所降低。

绝热过程中$Q=0$，对于理想气体，不做非膨胀功时：

$$
dU = C_VdT = \partial W
$$

若$C_V$为常数：

$$
W = \Delta U = C_V(T_1-T_2)
$$

上式可计算理想气体在绝热过程中的功。

在绝热过程中，理想气体所遵从的$p \sim V$的关系与等温过程不同，称为绝热过程方程式（adiabatic process equation）:

$$
pV^{\gamma} = Constant
$$

数学推导

上式中的$\gamma = \frac {C_p}{C_V}$，称为热容比（heat capacity ratio）。

对于等温可逆过程，用$pV = K$表示；对于绝热可逆过程，用$pV^{\gamma} = K$表示（两个$K$不相同，但均为常数）。

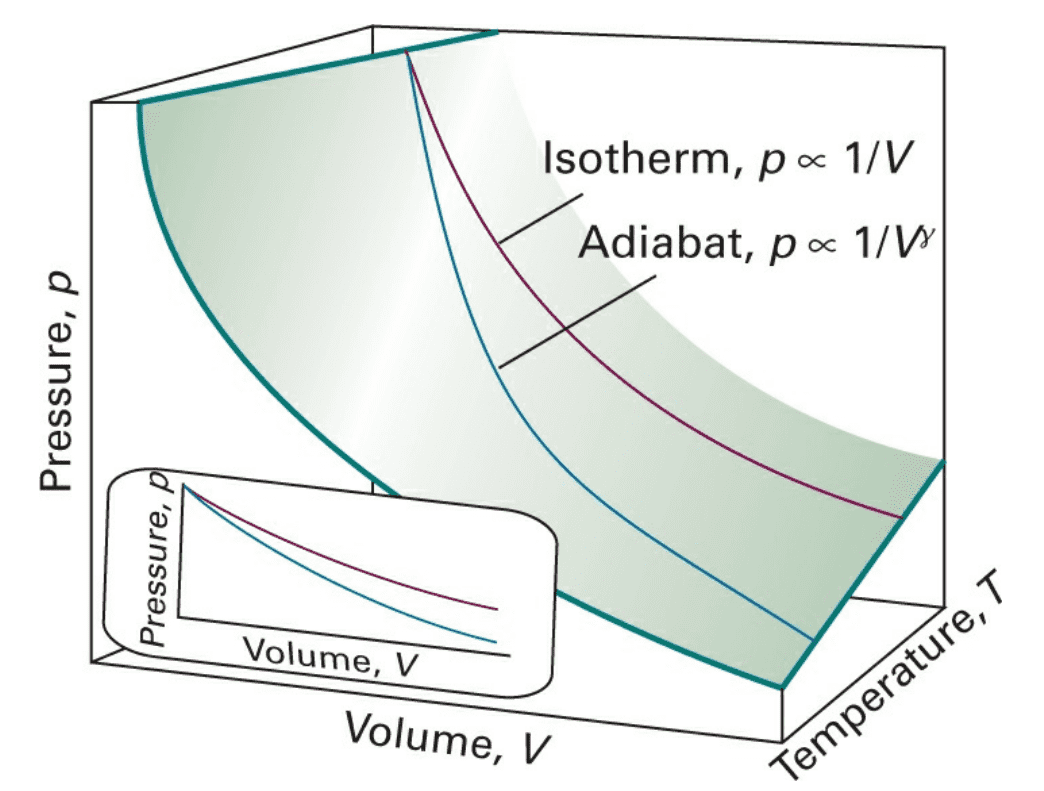
从图中也能看出，绝热可逆过程线的坡度比等温可逆过程线的坡度更陡，意味着相同的体积变化下，绝热膨胀过程中气体压力的降低要比等温膨胀过程中更为显著。

在绝热膨胀过程中，一方面气体的体积变大做膨胀功，另一方面气体的温度下降，这两个因素都使气体的压力降低。而在等温过程中却只有第一个因素。

有了气体绝热膨胀过程的$p \sim V$关系，自然就可以求出绝热可逆过程的功：

$$
W = \frac {p_2V_2 - p_1V_1}{\gamma -1}
$$

形式不同，但是结果相同，上式加以变形也可以得到前文提到的用热容计算的结果。

实际过程中没有严格的绝热或等温，都是介于二者之间，这种过程称为多方过程（polytropic process）：

$$
pV^{\delta} = Constant
$$

式中$\gamma > \delta >1$，$\delta$的数值越接近哪一边，则过程越接近对应过程。

2.9 Carnot循环

1824年，法国工程师N. L. S. Carnot设计了一个由两个等温过程和两个绝热过程构成的最简单的理想循环，后来被称为Carnot循环（Carnot cycle）。

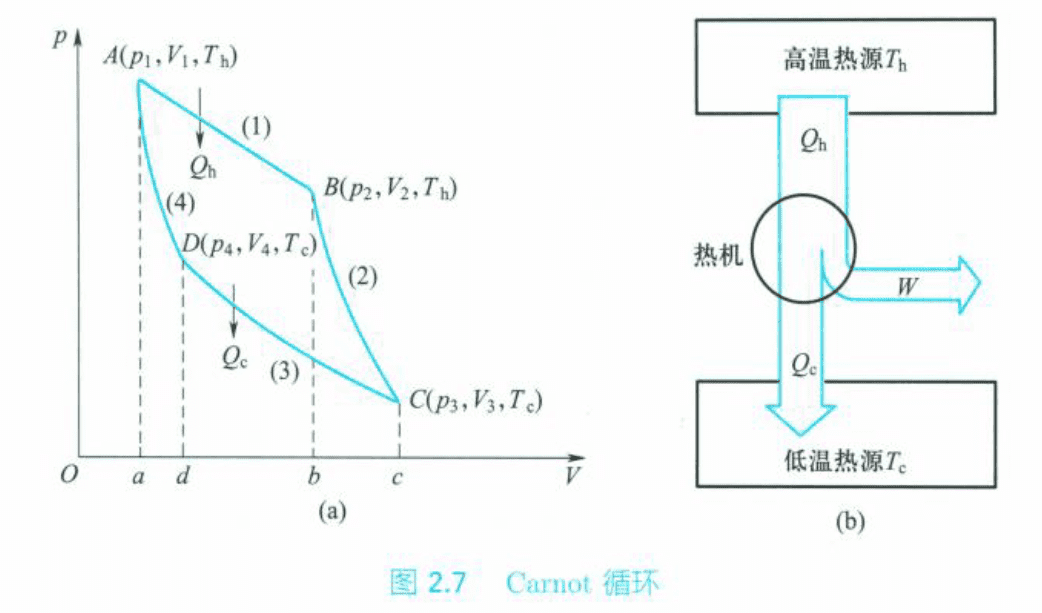
整个循环可以分为等温可逆膨胀-绝热可逆膨胀-等温可逆压缩-绝热可逆压缩。四个过程构成一个可逆循环，系统又回到了始态，根据热力学第一定律可以计算循环的功：

$$
W = W_1 + W_2 + W_3 + W_4 = W_1 + W_3 = nR(T_h-T_c)\ln\frac {V_1}{V_2}
$$

热机从高温热源吸热$Q_h$，仅将其中一部分转变为功，另一部分热$Q_c$传给低温热源。热机对环境所做的功与从高温热源所吸的热之比，称为热机效率（efficiency of heat engine），也称热机的转换系数（transformation coefficient）：

$$
\eta = \frac {-W}Q = 1- \frac {T_c}{T_h}
$$

可逆热机的转换系数只与两个热源的温度有关，两个热源的温度差越大，转换系数也越大，热量利用率也越高。

如果把可逆的Carnot机倒开，就变成制冷机或热泵。制冷机和热泵的原理是相同的，但是关注点不一样，制冷机关注的是把低温热源的热量移走，而热泵关注的是把热量运往高温热源。

2.10 Joule-Thomson效应——实际气体的$\Delta U$和$\Delta H$

在2.8节，介绍了Gay-Lussac - Joule实验，但是那个实验不够精确，因为环境热容量比气体大得多，不易观察到气体膨胀后温度是否发生了微小变化。因此在1852年，Joule和Thomson进行了另一个实验，使得我们对实际气体的$U,H$等性质有所了解。

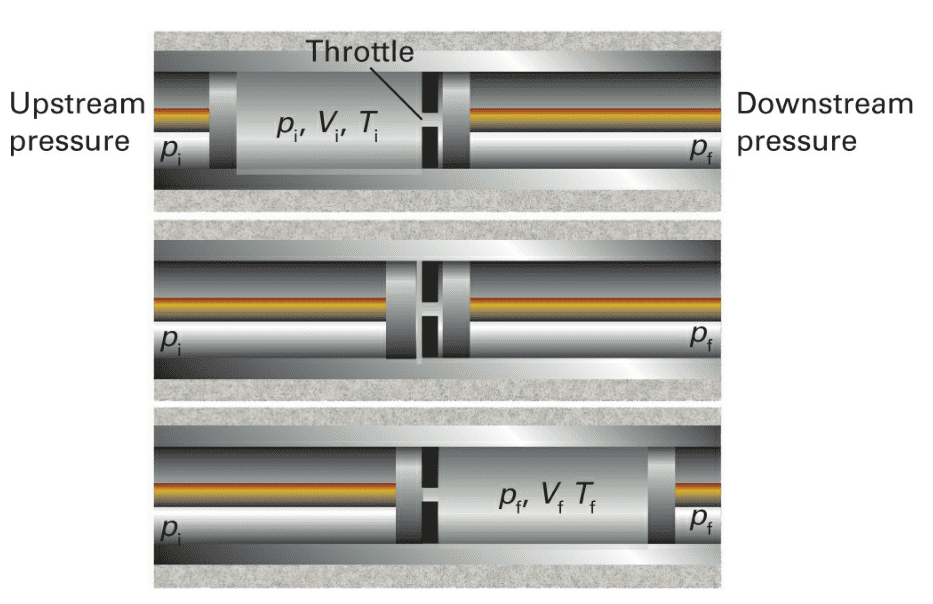
实验中气体从左侧通过一个多孔塞进入右侧，多孔塞使得两侧气体维持了一个压力差且使得气体慢慢通过，当气体通过一定时间达到稳态后，可以观察到双方气体的温度分别稳定于$T_1$和$T_2$，这个过程称为节流过程（throttling process）。Joule-Thomson实验验证了节流过程前后，气体的焓不变。

数学推导

气体经膨胀后的温度变化于压力变化的比值$\mu_{J-T}$用微分表示为：

$$
\mu _{J-T} = \left(\frac {\partial T}{\partial p} \right)_H
$$

$\mu {J-T}$称为Joule-Thomson系数，它表示经过Joule-Thomson试验后气体的温度随压力的变化率。一般而言，$\mu{J-T}$为正值，意味着气体随压力的降低，温度会下降；反之则压力降低后，气体的温度反而升高。

$\mu_{J-T}$是强度性质，是$T,p$的函数，随温度的改变而改变。理想气体的$\mu_{J-T}$恒为0，对实际气体来说，常温下一般气体的$\mu_{J-T}>0$，而$H_2,He$是例外，它们的$\mu_{J-T}$在常温下小于零，但是实验表明，在很低的温度下，它们的$\mu_{J-T}$也可转变为正值。当$\mu_{J-T}=0$时的温度称为转化温度（inversion temperature）。

数学推导

（ 从分子角度来考虑，气体温度的降低体现在气体分子的平均速率降低，考虑到实际气体分子间有相互作用力，如果分子间以吸引力为主导，气体在扩散时把动能转化为分子势能，动能减少，温度降低，此时$\mu>0$。反之亦然。

The kinetic model of gases and the equipartition theorem jointly imply that the mean kinetic energy of molecules in a gas is proportional to the temperature. It follows that reducing the average speed of the molecules is equivalent to cooling the gas. If the speed of the molecules can be reduced to the point that neighbours can capture each other by their intermolecular attractions, then the cooled gas will condense to a liquid.

Molecules in a real gas attract each other. It follows that, if the molecules move apart from each other, like a ball rising from a planet, then they should slow. It is very easy to move molecules apart from each other by simply allowing the gas to expand, which increases the average separation of the molecules. To cool a gas, therefore, expansion must occur without allowing any energy to enter from outside as heat. As the gas expands, the molecules move apart to fill the available volume, struggling as they do so against the attraction of their neighbours. Because some kinetic energy must be converted into potential energy to reach greater separations, the molecules travel more slowly as their separation increases, and the temperature drops. The cooling effect, which corresponds to $\mu > 0$, is observed in real gases under conditions when attractive interactions are dominant($Z<1,Z=V_m/V_m^{\ominus}$), because the molecules have to climb apart against the attractive force in order for them to travel more slowly. For molecules under conditions when repulsions are dominant ($Z>1$), the Joule–Thomson effect results in the gas becoming warmer, or $\mu < 0$.

）

如果多做几次实验，就可以获得多个焓值下的$(p,T)$状态，各点连接起来，就是一条等焓线（isenthalpic curve）。线上任一点的斜率就是该温度和压力下的Joule-Thomson系数。那么曲线最高点处斜率为0，也就是$\mu =0$，那么最高点的温度即为转化温度。

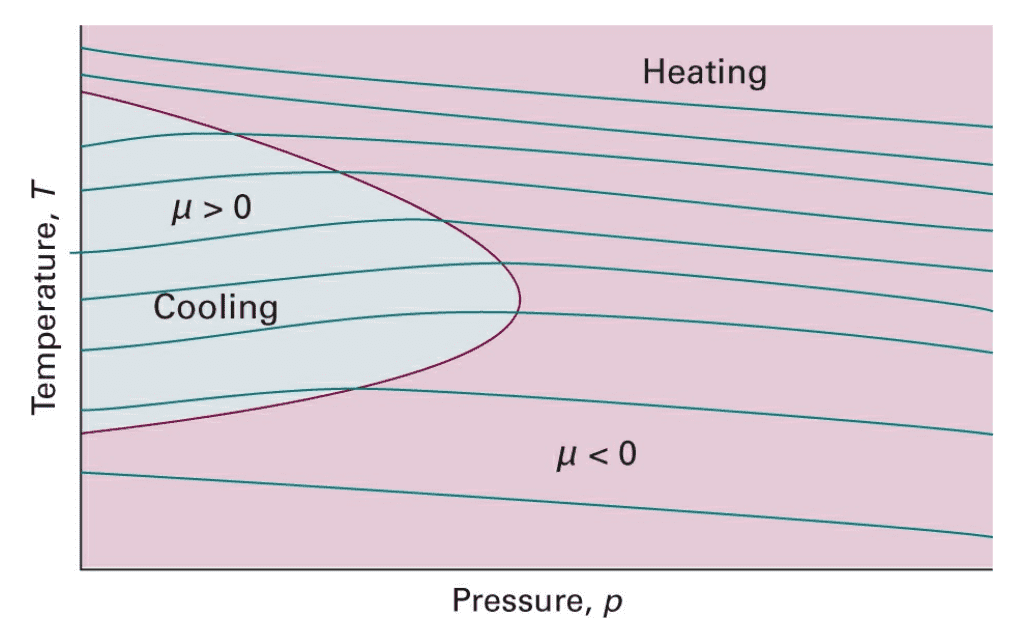
Joule-Thomson效应最重要的用途是用于使系统降温及使气体液化。

对于理想气体，$U/H$仅是$T$的函数，但是实际气体则不同，它们的热力学能/焓还与$V，p$有关:

$$
\Delta U = \int C_VdT + \int \frac a {V_m^2}dV
$$

数学推导

因为实际气体需要考虑分子间的作用力，所以用反抗分子间的引力即内压力（internal pressure）$p_i$所消耗的能量来衡量热力学能的变化：

$$
p_i = \left(\frac {\partial U}{\partial V} \right)_T \quad dU=p_idV
$$

若气体的状态符合van der Waals方程式：

$$
\left(p+\frac a{V_m^2} \right)\left(V_m - b\right)= RT
$$

根据下一章的Maxwell关系式可以推导出：

$$
p_i = \frac a {V_m^2}
$$

所以：

$$
dU = \left(\frac {\partial U}{\partial T}\right)_VdT+\left(\frac {\partial U}{\partial V}\right)_TdV = C_VdT+\frac {a}{V_m^2}dT
$$

所以可以看出，实际气体的内能表达式多了一个有关$a$的积分项，也就是内压力造成的影响。

2.11 热化学

（ 前面可以说都是物理内容，这部分开始进入化学知识了。不过热化学的基本内容都在基础无机里学过一遍了，这里也没有什么新东西，我就不多写了。 ）

对于理想气体，$H/U$仅是温度的函数，化学反应的热效应与其相关，在2.8节中，已经证明了等容热容和等压热容的关系，因此不难得出等容反应热和等压反应热的关系：

$$
Q_p = Q_V + \Delta n(RT)
$$

上式是从理想气体来出发推导的，对于其他物质，物理变化的过程的热效应对比化学反应热基本可以忽略不计，因此也可近似为上式。

然后引入反应进度（extent of reaction）$\xi$：

$$
d\xi = \frac {dn_B}{\nu_B}
$$

有了反应进度就可以计算摩尔焓变，这样就不会因方程式的写法不同而改变焓变数值。

再定义标准态的概念，压力为$100kPa$，温度没有指定温度，但是常用$298.15K$，物质需要是纯物质。这样就有了标准态的概念，也就有了标准摩尔焓变。

2.12 Hess定律

反应的热效应只与始态和终态有关，而与变化途径无关，这就是Hess定律（Hess’s law），因此可以把热化学方程式加减来计算目标反应的焓变。

2.13 几种热效应

标准摩尔生成焓、用键焓估计反应焓、标准摩尔离子生成焓、标准摩尔燃烧焓、溶解热和稀释热，大部分都是基础无机讲过的，少部分没提过但是可以类比着理解。

2.14 反应焓变与温度的关系——Kirchhoff定律

等压下，若使同一化学反应分别在两个不同的温度$T_1$和$T_2$下进行，所产生的热效应一般不同，$\Delta H$和温度的关系如下：

$$
\Delta_rH_m(T_2) = \Delta_rH_m(T_1) + \int_{T_1}^{T_2} \Delta C_pdT \[3mm] \Delta C_p = \sum_B\nu_BC_{p.m}(B)
$$

数学推导

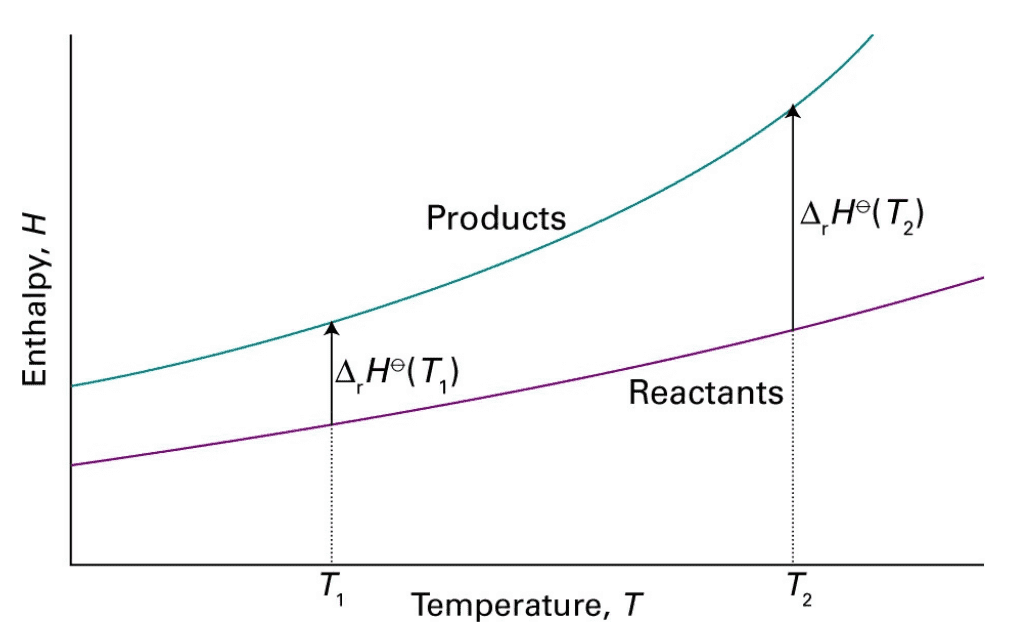
如上图，对于反应物和生成物分别可以写出：

$$
H(T_2) = H(T_1) + \int_{T_1}^{T_2} C_pdT
$$

两式作差即得反应焓：

$$
\Delta_rH^{\ominus}(T_2) = \Delta_rH^{\ominus}(T_1) + \int_{T_1}^{T_2} \Delta_r C_p^{\ominus}dT \[3mm] \Delta_r C_p^{\ominus} = \sum_{Products}\nu C_{p,m}^{\ominus} - \sum_{Reactants}\nu C_{p,m}^{\ominus}
$$

把热容写成级数展开的经验形式，因此可以求得焓变和温度的关系：

$$
\Delta_rH_m(T) = \Delta aT + \frac 1 2\Delta bT^2 - \Delta c’ \frac 1T + \cdots + Constant
$$

2.15 绝热反应——非等温反应

在2.8节已经讨论了绝热过程，绝热反应也具有相同的原理，反应在绝热情况下进行，系统的终态温度要发生改变。

利用Hess定律往往可以绕圈子来求得目标反应的焓变，然后就可以求得反应终态温度。

2.16 热力学第一定律的微观诠释

考虑系统发生了微小变化，那么热力学能的变化为：

$$
dU= \delta Q + \delta W
$$

假设构成系统的粒子彼此之间势能很小，可以忽略，这种系统就称为近独立子系统。

设粒子总数为$N$，分布在不同能级$\epsilon_i$上，并设在能级$\epsilon_i$上的粒子数为$n_i$，则：

$$
N = \sum_in_i \quad U = \sum_in_i\epsilon_i
$$

对上式微分：

$$
dU = \sum_in_id\epsilon_i + \sum_i\epsilon_idn_i
$$

该式与热力学第一定律相对照，那么右侧两相必然分别于热和功相联系。

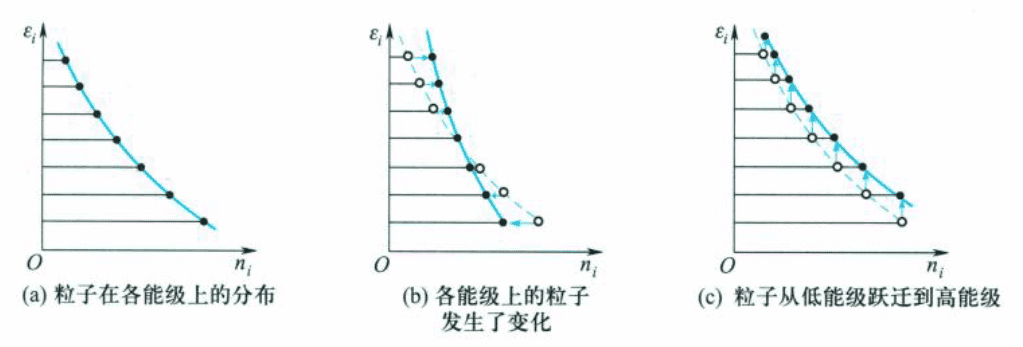
可以推导出，功来源于能级的改变，但是各能级上粒子数不变而引起的能量变化，见上图（c），对应式中右侧第一项；而热是由于粒子在能级上重新分布而引起的热力学能的改变，见上图（b），对应式中右侧第二项。

（ 从中可以体会一下2.3节中提到的，功是粒子有序运动，而热是粒子无序运动。 ）

物质的热容与热力学能密切相关，而热力学能包括内部各种能量的总和，但是对于单分子气体，一般只考虑平动动能；双原子分子还要考虑转动和振动。

根据能量均分定理（principle of energy equipartition），能量均匀分布在每个自由度上，可知单原子分子的等容热容$C_{V,m}=\frac 32R$，双原子分子常温的等容热容$C_{V,m}=\frac52R$。

2.17 由热力学第零定律导出温度的概念

根据热力学第零定律，互为热平衡的系统必定拥有一个共同的物理性质，表征这个物理性质的量就是温度。本节通过数学方法导出温度的概念。

数学推导

2.18 关于以J（焦耳）作为能量单位的说明

用$J$作为单位的优越性表现在电流的热效应能够方便的测量，而之前的单位$cal$与水的比热有关，计算很是麻烦。后来将$cal$的定义重新修正：

$$
1cal(热化学)=4.184J
$$

这样$cal$就是一个规定值，与水的比热没有联系了。

总结

写到最后我的编辑器都开始卡了，字数已经18000+，似乎已经超过了无机下册最多的一章了。

不过也没办法，毕竟这一章内容确实多，我写得也确实累 :(

第二章是热力学部分，而且大部分内容与基础无机重合，考虑到热力学是物化的主要讨论内容，加深理解还是很重要的。