《物理化学》章末总结13

十三章表面物理化学，大多数内容都是了解即可。

第十三章 表面物理化学

密切接触的两相之间的过渡区称为界面（interface），根据物质状态的不同，界面可以分为气-液、气-固、液-液、液-固和固-固等界面。前两种界面都有气体参加，此类界面习惯上常称为表面（surface），但实际上没有严格区分。

界面不是一个没有厚度的纯粹几何面，它有一定的厚度，可以是单分子层的，也可以是多分子层的，这一层的性质往往与临近的两侧大不一样。

在研究表面层上发生的行为或者研究多相的高分散系统的性质时，必须考虑物质的分散度（dispersion degree）。通常用比表面（$A_0$）来表示分散程度。

$$
A_0 = \frac {A_s}{m}
$$

比表面即是单位质量物质的表面积，类似的，比表面还可以用单位体积物质的表面积表示。

13.1 表面张力及表面Gibbs自由能

液体表面的最基本特性是趋向收缩，如液滴趋向于呈球形，这就是表面张力的作用。测定表面张力的方法有很多，如毛细管上升法、滴重法、最大泡压法等等。

由于表面张力的存在，如果要增加液体的表面积，必须要考虑液体的表面功，因此我们可以得到热一和热二定律联合公式的补充：

$$
dU = TdS - pdV + \gamma dA_s + \sum_B \mu_B dn_B
$$

同理可得其他热力学函数的表示，从而：

$$
\gamma = \left(\frac {\partial U}{\partial A_s} \right){S,V,n_B} = \left(\frac {\partial H}{\partial A_s} \right){S,p,n_B} = \left(\frac {\partial A}{\partial A_s} \right){T,V,n_B} = \left(\frac {\partial G}{\partial A_s} \right){T,p,n_B}
$$

可知$\gamma$是指在各相相应变量不变的情况下，每增加单位表面积时，系统热力学能或Gibbs自由能等热力学函数的增值，称为广义的表面自由能。

温度升高时，界面张力总是下降，这可从基本公式中看出：

$$
T\left(\frac {\partial S}{\partial A_s} \right){T,V,n_B} = -T\left(\frac {\partial \gamma}{\partial T} \right){A_s,V,n_B} > 0
$$

即$\partial \gamma/\partial T <0$，说明$\gamma$的值会随$T$的升高而下降。

水的表面张力因加入溶质形成溶液而改变，有些溶质加入后使溶液的表面张力降低，有些溶质则使溶液的表面张力升高。前者称为表面活性物质（surface active agent），后者称为非表面活性物质（non-surface active agent）。能使水的表面张力降低的溶质都是有机化合物，但习惯上只把那些明显降低水的表面张力的两亲性质的有机化合物叫做表面活性剂。

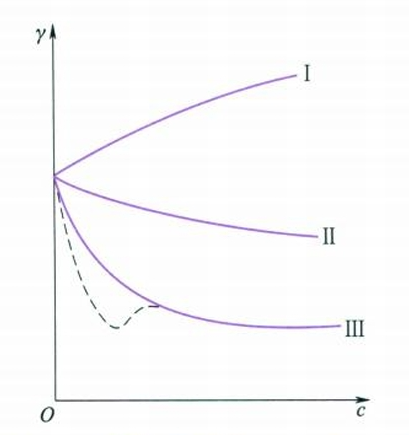
对于脂肪酸同系物，每增长一个$CH_2$其表面张力降低效应平均可增加约3.2倍，称为Traube规则。但是Traube规则不能包括所有的表面张力随浓度的变化情况，根据实验，稀溶液的$\gamma - c$曲线类型可见下图：

13.2 弯曲表面上的附加压力和蒸气压

（ 本节讨论的内容只适用于曲面半径较表面层的厚度大得多的情况。 ）

由于表面张力的作用，在弯曲表面下液体或气体与在平面下情况不同，前者受到附加压力。

静止液体一般是一个平面，但是在某些特殊情况下（如在毛细管中）呈弯曲表面，由于表面张力方向沿界面切向，因此弯曲表面的内、外受力不等。附加压力的方向指向曲面圆心。

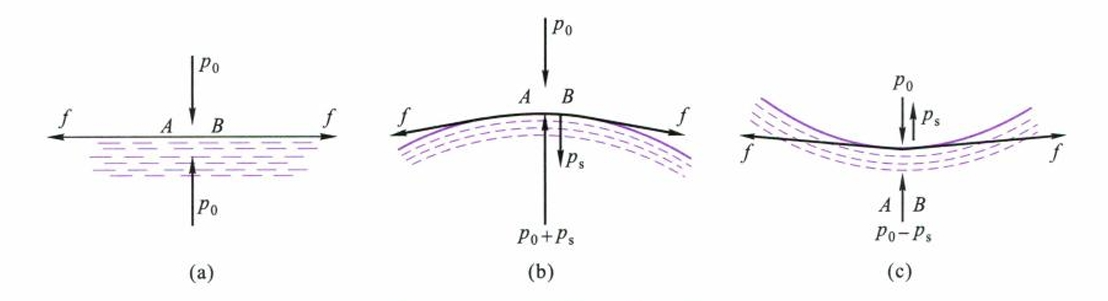
附加压力方向与曲率半径有关，通过凸形液滴推导可得：

$$
p_s = \frac {2\gamma}{R’}
$$

曲率半径越小，则液滴所受的附加压力就越大；液滴呈凸形，附加压力与外压方向一致，液滴呈凹形，附加压力与外压方向相反。

知道了这一点，我们就能解释一些常见的现象，例如自由液滴或气泡在不受外加力场影响时通常成球形，因为对于不规则的形状，其在表面上不同位置所受的附加压力也不同，这种不平衡的力必定使得液滴变为球形。因为球面上各点的曲率相同，各处的附加压力也相同，液滴才会成稳定的形状。

毛细管中液体产生液面高度差的现象也是由于附加压力引起的，可近似用如下公式计算：

$$
\frac {2\gamma \cos \theta}{R} = \Delta \rho gh
$$

弯曲曲面上的附加压力可以用Young-Laplace公式描述：

$$
p_s = \gamma \left(\frac {1}{R_1’} + \frac {1}{R_2’} \right)
$$

曲面施于液体的附加压力随曲率而变，所以不同曲率的曲面所包围的液体的状态并不相同，例如平面液体与曲面液体上的蒸气压就不同。

对于弯曲表面上的蒸气压可以用Kelvin公式描述：

$$
RT\ln \frac {p_r}{p_0} = \frac {2\gamma M}{R’\rho}
$$

此式说明液滴越小，蒸气压越大，同时还可以解释一些常见现象，如为什么蒸汽凝结需要凝聚中心。因为如果无凝聚中心，形成的小液滴的蒸气压大，难以形成，而凝聚中心的存在绕过了产生极微小气泡的困难阶段，因此利于液体凝结。

13.3 溶液的表面吸附

溶液看起来非常均匀，但实际上并非如此，表面上一薄层的浓度比内部更高，这种差别称为表面过剩（surface excess）。

Gibbs用热力学方法研究了表面过剩现象，并导出了Gibbs吸附公式：

$$
\Gamma_B = -\frac {a_B}{RT} \frac {d\gamma}{da_B}
$$

具体的推导细节在此略去。

13.4 液-液界面的性质

首先讨论液-液界面的铺展，即一种液体是否能在另一不互溶的液体上铺展（spreading）开，取决于各液体自身的表面张力和两液体之间界面张力的大小。

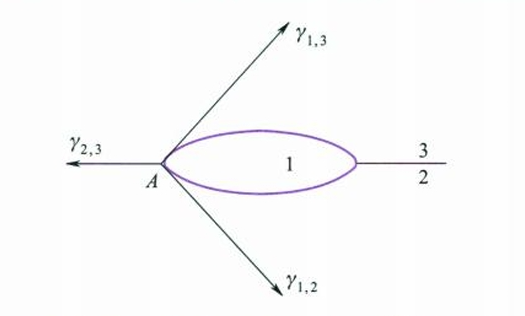
图中3为气相，1和2为两种不互溶液体，考虑图中A点处，$\gamma_{1,3}$和$\gamma_{1,2}$的作用是力图维持液滴成球形，而$\gamma_{2,3}$的作用是力图使液体铺展开来，因此，如果满足：

$$
\gamma_{2,3} > \gamma_{1,3} + \gamma_{1,2}
$$

则液体1可以在液体2上铺展开来。

两亲分子在水上铺展形成的表面膜称为铺展膜（spread film），它是定向的单分子膜，这种二维空间不溶性单分子表面膜的应用是多方面的，如降低水蒸发速率、测定蛋白质分子的摩尔质量、使化学平衡发生移动等。

13.5 膜

若将单分子膜转变为L-B膜，则用途更为广泛。L-B膜由Langmuir和他的学生Blodgett女士首创，故称L-B膜。L-B膜是一种具有相对规整的分子排列、高度各向异性的层结构，以及人为可控的纳米尺度的薄膜。

L-B膜在电子器件制造、非线性光学器材、广电转化器件等方面都有重要作用，潜力巨大。

细胞是体现生物体生命活动和各种功能的最基本单位，细胞有一层很薄的细胞膜，它把细胞内的物质与周围环境分隔开来。

生物膜在生物体内起着分离、信息传递、蛋白质合成等功能，许多生命过程中的重要反应都是在体内的各种生物膜上进行的。

13.6 液-固界面——润湿作用

在固体上滴上少许液体，液体取代了部分固-气界面，生成新的固-液界面，这一过程称为润湿过程（wetting）。

润湿过程可以分为三类，即黏湿（aadhesion）、浸湿（immersion）和铺展（spreading），下面分别介绍。

黏湿是指液体和固体从不接触到接触，使部分气-液界面和气-固界面转变成新的液-固界面的过程。

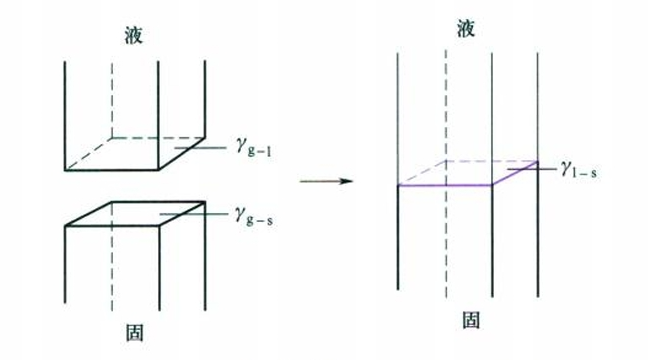
该过程的Gibbs自由能变为：

$$
W_a = \Delta G = \gamma_{l-s} - \gamma_{g-l} - \gamma_{g-s}
$$

当$\Delta G \le 0$时黏湿过程自动进行，$W_a$的绝对值越大，液体越容易黏湿固体。

浸湿是指将固体浸入液体中，气-固界面转变为液-固界面的过程。

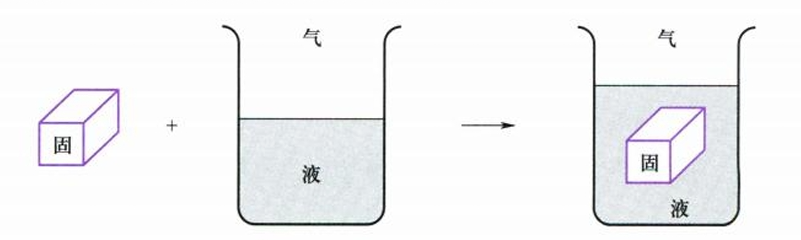
该过程的Gibbs自由能变为：

$$
W_i = \Delta G = \gamma_{l-s} - \gamma_{g-s}
$$

当$\Delta G \le 0$时液体能浸湿固体，$W_i$称为浸湿功。

铺展是指液体滴到固体表面后，新生的液-固界面取代气-固界面的同时，气-液界面也扩大了同样的面积的过程。

该过程的Gibbs自由能变为：

$$
S = -\Delta G = \gamma_{g-s} - \gamma_{g-l} - \gamma_{l-s}
$$

当$\Delta G \le 0$，即$S \ge 0$时，液体可以在固体表面自动铺展，$S$称为铺展系数（spreading coefficient）。

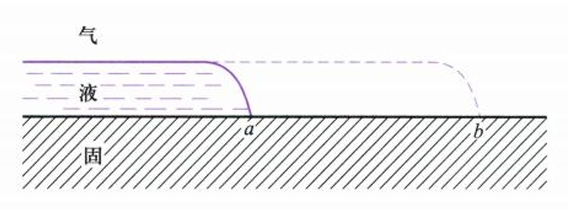
对于上述三种具体的润湿过程，我们可以具体分析，同时，我们也可以从更一般的情况考虑，引入接触角（contact angle）的概念，判断液体对固体润湿的程度。

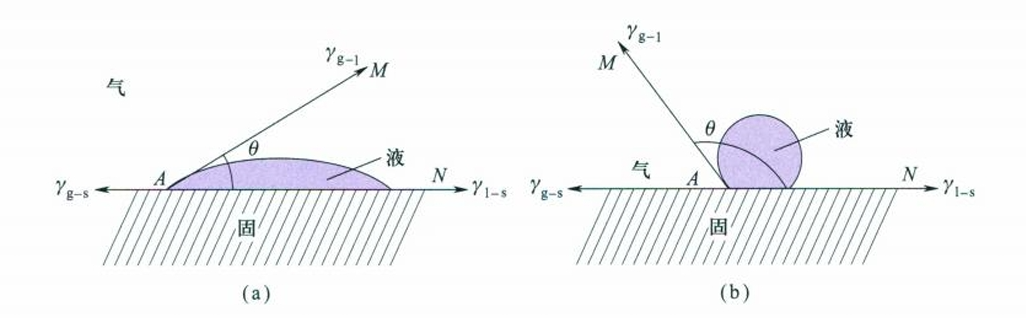
在气、液、固三相交界处，气-液界面与液-固界面之间的夹角称为接触角，接触角的大小是由在气、液、固三相交界处三种界面张力的相对大小所决定的。

T. Young最早提出了杨氏润湿方程来计算接触角：

$$
\cos \theta = \frac {\gamma_{g-s} - \gamma_{l-s}}{\gamma_{g-l}}
$$

进一步可得：

$$
W_a = -\gamma_{g-l} (1 + \cos \theta) \[3mm]
W_i = - \gamma_{g-l} \cos \theta \[3mm]
S = \gamma_{g-l} (\cos \theta -1)
$$

据此可得润湿过程能否进行与接触角间关系。

13.7 表面活性剂及其作用

某些物质以低浓度存在于某一系统（通常是指水为溶剂的系统）中时，可被吸附在该系统的表面上，使这些表面的表面张力发生明显降低的现象，这些物质被称为表面活性剂（surfactant）。

表面活性剂一般分为离子型和非离子型两种，更详细的分类可见下图。

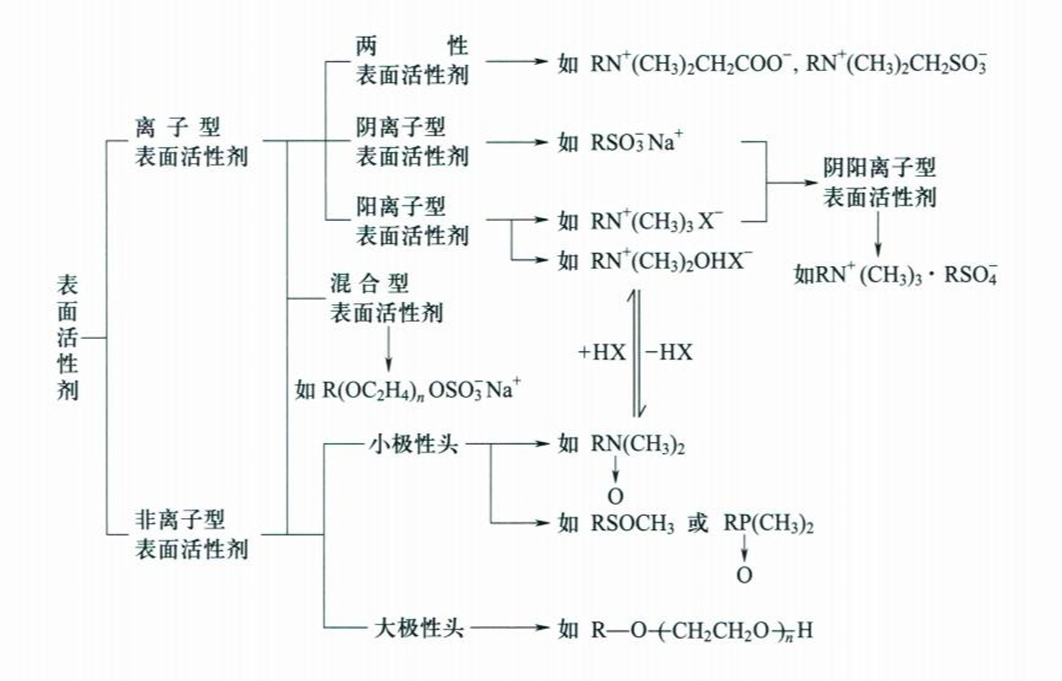
关于表面活性剂的结构与性质关系，性能评价等内容在此略去。

表面活性剂在生产活动中经常发挥重要作用，如人为控制固、液之间的润湿程度、利用表面活性剂来起泡/消泡、增加不溶物在水中的溶解度、乳化洗涤等。

13.8 固体表面的吸附

我们在前文提到过，液体表面由于受力不均匀，因此有收缩表面的倾向。固体表面同样受力不均，但是由于固体分子或原子不能自由移动，无法收缩表面来减小表面能，因此表现出与液体不同的吸附分子的能力。

当气体在固体表面被吸附时，固体叫吸附剂（absorbent），被吸附的气体叫吸附质（adsorbate）。实验表明，对于一个给定的系统，达到平衡时的吸附量$q$与温度及气体的压力有关：

$$
q = f(T,p)
$$

为了说明上式中三个变量的关系，常固定其中一个，然后求出其他两个变量间的关系，例如，当温度$T$不变，则$q=f§$，称为吸附等温式（adsorption isotherm）。类似的，固定压力$p$可得吸附等压式（adsorption isobar）；固定吸附量$q$可得吸附等量式（adsorption isotere）。

从一组曲线可以画出另外两种，最常用的是吸附等温线。

根据实验结果，人们发现各种吸附等温线主要包含如下五种类型：

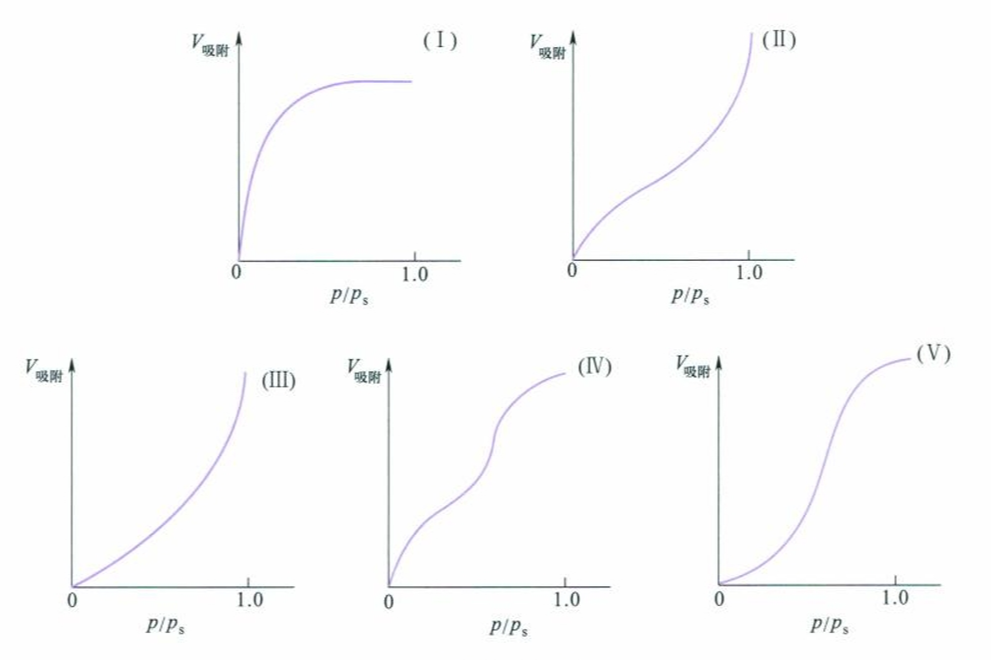
吸附等温线的不同反映了吸附剂的表面性质有所不同，孔分布及吸附质和吸附剂的相互作用不同。

Langmuir在研究低压下气体在金属上的吸附时，根据实验数据发现了一些规律，然后又从动力学的观点提出了一个吸附等温式，并总结出Langmuir单分子层吸附理论。

该理论的基本观点是，气体在固体表面上的吸附作用是气体分子在吸附剂表面吸附与解吸两种相反过程达到动态平衡的结果。

他在推导过程中提出了两个基本假定：吸附是单分子层的；已被吸附的分子之间不互相影响。

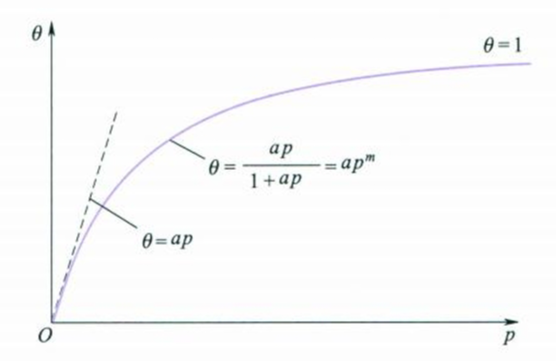
据此，他给出了Langmuir吸附等温式：

$$
\theta = \frac {ap}{1+ap}
$$

式中$\theta$为表面覆盖率，$a=k_a/k_d$，即吸附过程的速率常数比脱附过程的速率常数，称为吸附系数（adsorption coefficient），$p$为平衡压力。

不难看出，当压力很低时，上式可简化为$\theta \approx ap$，即$\theta$与$p$成线性关系；当压力足够高时，上式可简化为$\theta \approx 1$，即$\theta$与$p$无关。如下图所示：

对于混合气体的表面吸附，可推广得到：

$$
\theta_B = \frac {a_Bp_B}{1+\sum_B a_Bp_B}
$$

（ 推导过程在此略去。 ）

除了Langmuir外，还有其他人提出的一些等温式，如Freundlich吸附等温式、Temkin方程式和BET多层吸附公式等，在此仅给出公式。

$$
q = kp^{1/n} \quad (Freundlich\ isotherm)\[3mm]
\theta = \frac {RT}{\alpha} \ln (A_0 p) \quad (Temkin\ isotherm) \[3mm]
V = V_m \frac {C_p}{(p_s - p) \left[1+(C-1) \frac {p}{p_s} \right]} \quad (BET\ isotherm)
$$

以上内容讨论了吸附作用的一般现象，我们需要进一步探索吸附现象的本质问题，即究竟是什么作用使气体分子可以吸附在固体表面上。

根据吸附分子与固体表面作用力性质的不同，可以把吸附分为两类，一是物理吸附（physical adsorption），一是化学吸附（chemical adsorption）。二者的比较见下表。

	物理吸附	化学吸附
吸附力	van der Waals力	化学键力
吸附热	较小，从几百到几千焦每摩尔	较大，一般大于几万焦每摩尔
选择性	无选择性	有选择性
吸附稳定性	不稳定，易解吸	比较稳定，不易解吸
分子层	单分子或多分子层	单分子层
吸附速率	较快，不需要活化能	较慢，需要活化能

两类吸附常常同时发生，不能认为某一吸附只有化学吸附没有物理吸附，反之亦然。

二者的本质不同来自于吸附力的性质不同，物理吸附是van der Waals力的作用，而化学吸附则是化学键的形成，从这一点出发，那么物理吸附和化学吸附的许多不同都易于理解了。

13.9 气-固相表面催化反应

大量经验事实表明，气-固相多相催化反应是反应物分子首先吸附在固体表明的某些部位上，形成活化的表面中间化合物，使反应的活化能降低，反应加速，然后脱附得到产物。

当表面反应为速控步骤时，讨论其速率方程表达式，篇幅所限，本文只讨论单分子反应。

假定吸附和解吸的速率都很快，而表面反应速率较慢，且产物吸附很弱，能够快速脱附，则可推得：

$$
r = \frac {ka_Ap_A}{1+a_Ap_A}
$$

式中$k$为表面反应的速率常数，$a_A$为物种A的吸附常数。

类似于Langmuir吸附，当压力很低时，$a_Ap_A \ll 1$，则$r=ka_Ap_A$，反应表现为一级反应；如果反应物压力相当大，$a_Ap_A \gg 1$，则$r=k$，即为零级反应；若反应压力适中，则反应级数也介于0到1之间。

对于双分子反应可能有两种反应历程，一是Langmuir-Hinshelwood历程（L-H历程），一是Rideal历程，二者的主要差别是前者的两种粒子都在表面吸附并发生反应，而后者的其中一种粒子未发生吸附。

二者的不同还可以从反应速率与分压图中看出，更进一步的内容在此略去。

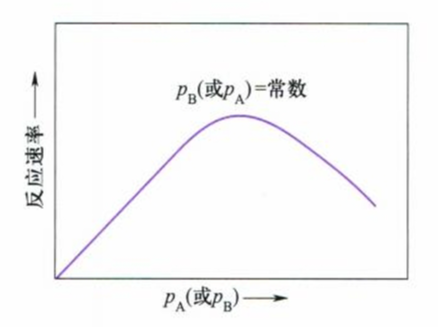
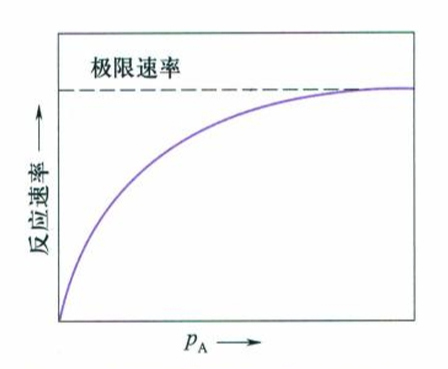
总结

表面物理化学无疑是有很多内容可谈的，可以说是催化的核心原理之一，不可谓不重要。但是本章在教学安排上是比较紧张的，只能是草草过一遍完事，就连我这个post还是放假之后才补上的，可能是因为考试考的相对比较少吧。