《Quantum Chemistry》章末总结1

量子化学系列，使用的教材是Donald A. Mcquarrie的Quantum Chemistry 2nd，同时配套MIT公开课的5.61 Physical Chemistry一起学。

正式开始前多说几句，国内本科阶段通常会设置一门课叫结构化学，而国外大学是没有这门课的。结构化学的授课内容基本上是量子化学基础+其他零碎的知识，比如晶体学，光谱，配合物，固体物理的一些初级部分，这种杂糅的内容安排使得这门课程内容覆盖比较广泛，但也造成了其系统性和整体性的缺乏。再考虑到北大那本结构教材写的实在是不尽人意，一学期的结构化学上下来，我也很难说自己学到了什么。所以在选择学习教材时，我选了这本更基础的教材，而没有用Levine的那本量子化学。

Chapter 1 The Dawn of the Quantum Chemistry

1.1 Blackbody Radiation Could Not Be Explained by Classical Physics

The exact frequency spectrum emitted by the body depends on the particular body itself, but an ideal body , which absorbs and emits all frequencies, is called a blackbody and serves as an idealization for any radiating material. The radiation emitted by a blackbody is called blackbody radiation.

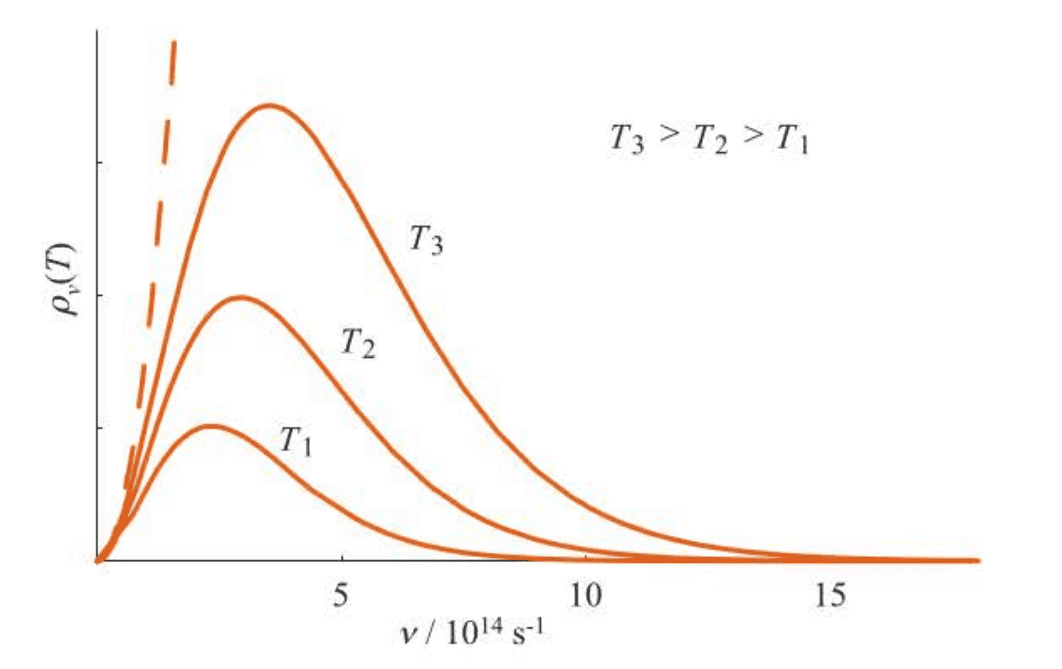
A plot of the intensity of blackbody radiation versus frequency for several temperatures is given in Figure 1.1. Many theoretical physicists tried to derive expressions consistent with these experimental curves of intensity versus frequency, but they were all unsuccessful. In fact, the expression that is derived according to the laws of nineteenth century physics is:

$d\rho(\nu,T)=\rho_{\nu}(T)d\nu=\frac {8\pi k_BT}{c^3}\nu^2d\nu$

The equation came from the work of Lord Rayleigh and J. H. Jeans and is called the Rayleigh-Jeans law. The dashed line in Figure 1.1 shows the prediction of the Rayleigh-Jeans law. Note that the Rayleigh-Jeans law reproduces the experimental data at low frequencies. At high frequencies, however, the Rayleigh-Jeans law predicts that the radiant energy density diverges as $\nu^2$. Because the frequency increases as the radiation enters the ultraviolet region, this divergence was termed the ultraviolet catastrophe, a phenomenon that classical physics could not reconcile theoretically.

（ 经典的紫外灾难，每次讲黑体辐射必定会有这个公式，它也确实反应了在那个时代经典物理学遇到的难题。 ）

Many other people reproduced the equation of Rayleigh and Jeans, showing that this equation was correct according to the physics of the time. This result was very disconcerting, and many people struggled to find a theoretical explanation of blackbody radiation.

1.2 Planck Used a Quantum Hypothesis to Derive the Blackbody Radiation Law

The first person to offer a successful explanation ofblackbody radiation was the German physicist Max Planck in 1900. Implicit in the derivation of Rayleigh and Jeans is the assumption that the energies of the electronic oscillators responsible for the emission of the radiation could have any value whatsoever. This assumption is one of the basic assumptions of classical physics. In classical physics, the variables that represent observables (such as position, momentum, and energy) can take on a continuum of values. Planck had the great insight to realize that he had to break away from this mode of thinking to derive an expression that would reproduce experimental data.

He made the revolutionary assumption that the energies of the oscillators were discrete and had to be proportional to an integral multiple of thefrequency or, in equation form, that $E=nh\nu$. Using this quantization of energy and some statistical thermodynamic ideas, Planck derived the equation.

$d\rho(\nu,T)=\rho_{\nu}(T)d\nu=\frac{8\pi h}{c^3} \frac {\nu^3d\nu}{e^{h\nu/k_BT}-1}$

Planck showed that this equation gives excellent agreement with the experimental data for all frequencies and temperatures if $h$ has the value $6.626 \times 10^{-34}$ joule· seconds ($J\cdot s$). This constant is now one of the most famous and fundamental constants of physics and is called the Planck constant.

（ 普朗克革命性的提出了量子化的概念，无疑是量子力学的开创人，不过他在最初提出黑体辐射公式的时候，也不是直接就提出了能量量子化的概念，而是先“凑”出符合实验的结论再回过头来分析才得出的。当然说是“凑”公式，实际上还是离不开普朗克良好的数学、物理尤其是热力学的掌握。 ）

The theory of blackbody radiation is used regularly in astronomy to estimate the surface temperatures of stars. The star Sirius, which appears blue, has a surface temperature of about 11000$K$.

Nevertheless, Planck’s derivation and, in particular, Planck’s assumption that the energies of the oscillators have to be an integral multiple of $h\nu$ was not accepted by most physicists at the time and was considered to be simply an ad hoc derivation. It was felt that in time a satisfactory classical derivation would be found.

1.3 Einstein Explained the Photoelectric Effect with a Quantum Hypothesis

In 1886 and 1887, while carrying out the experiments that supported Maxwell’s theory of the electromagnetic nature of light, the German physicist Heinrich Hertz discovered that ultraviolet light causes electrons to be emitted from a metallic surface. The ejection of electrons from the surface of a metal by radiation is called the photoelectric effect.

Two experimental observations of the photoelectric effect are in stark contrast with the classical wave theory of light.

According to classical physics, electromagnetic radiation is an electric field oscillating perpendicular to its direction of propagation, and the intensity of the radiation is proportional to the square of the amplitude of the electric field. As the intensity increases, so does the amplitude of the oscillating electric field. The electrons at the surface of the metal should oscillate along with the field and so, as the intensity (amplitude) increases, the electrons oscillate more violently and eventually break away from the surface with a kinetic energy that depends on the amplitude (intensity) of the field. This classical picture is in complete disagreement with the experimental observations. Experimentally, the kinetic energy of the ejected electrons is independent of the intensity of the incident radiation.

Furthermore, the classical picture predicts that the photoelectric effect should occur for any frequency of light as long as the intensity is sufficiently high. The experimental fact, however, is that there is a threshold frequency, $\nu_0$, characteristic of the metallic surface, below which no electrons are ejected, regardless of the intensity of the radiation.

（ 光电效应实验的两个现象从经典物理学的角度都无法解释，这非常困惑当时的物理学家们，直到爱因斯坦借用了普朗克量子化的观点才给出一个圆满的解释。 ）

To explain these results, Albert Einstein used Planck’s hypothesis but extended it in an important way. Planck believed that once the light energy was emitted, it behaved like a classical wave. Einstein proposed instead that the radiation itself existed as small packets of energy, $E=h\nu$, now known as photons. Using a simple conservation-of-energy argument, Einstein showed that the kinetic energy (KE) of an ejected electron is equal to the energy of the incident photon ($h\nu$) minus the minimum energy required to remove an electron from the surface of the particular metal ($\phi$).

$KE=\frac 12mv^2=h\nu -\phi$

where $\phi$, called the work function of the metal, is analogous to an ionization energy of an isolated atom. The minimum frequency that will eject an electron is just the frequency required to overcome the work function of the metal. Thus, there is a threshold frequency, $\nu_0$, given by:

$h\nu_0=\phi$

（ 爱因斯坦的量子化假设给出的$h$值与普朗克得到的$h$值完全相等，这是一个有力的证据，许多当时的科学家们据此开始意识到这种量子化的假设是有其意义的。爱因斯坦也因为他在光电效应方面的工作于1921年获得诺贝尔物理学奖。 ）

1.4 The Vibrations of Atoms in Crystals Are Quantized

The law of Dulong and Petit says that the molar heat capacity at constant volume, $C_V$, is equal to $3R$. This is the standard classical result for the heat capacity of one mole of atoms vibrating about their equilibrium lattice positions. The experimental molar heat capacity, however, looks like that shown in Figure 1.2.

The classical result is seen to occur at high temperatures, but $C_V$ decreases and goes to zero as the temperature is lowered.

Einstein assumed that the oscillations of the atoms about their equilibrium lattice positions are quantized according to the formula $\epsilon=nh\nu$ or $\Delta \epsilon=h\nu$. With this assumption, Einstein was able to achieve excellent agreement with the data shown in Figure 1.2 by using only the vibrational frequency $\nu$ as an adjustable parameter.

1.5 The Hydrogen Atomic Spectrum Consists of Several Series of Lines

Each atom has a characteristic emission spectrum. Because the emission spectra of atoms consist of only certain discrete frequencies, they are called line spectra. Hydrogen, the lightest and simplest atom, has the simplest spectrum.

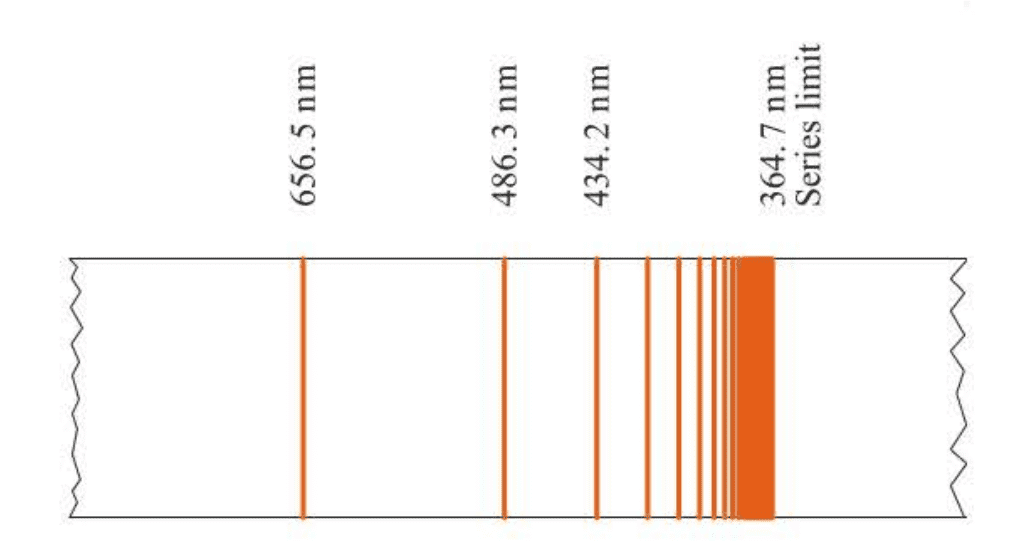
Because atomic spectra are characteristic of the atoms involved, it is reasonable to suspect that the spectrum depends on the electron distribution in the atom. For many years, scientists had tried to find a pattern in the wavelengths or frequencies of the lines in the hydrogen atomic spectrum. Finally, in 1885, an amateur Swiss scientist, Johann Balmer, showed that a plot of the frequency of the lines versus $1/n^2(n=3,4,5,\cdots)$ is linear.

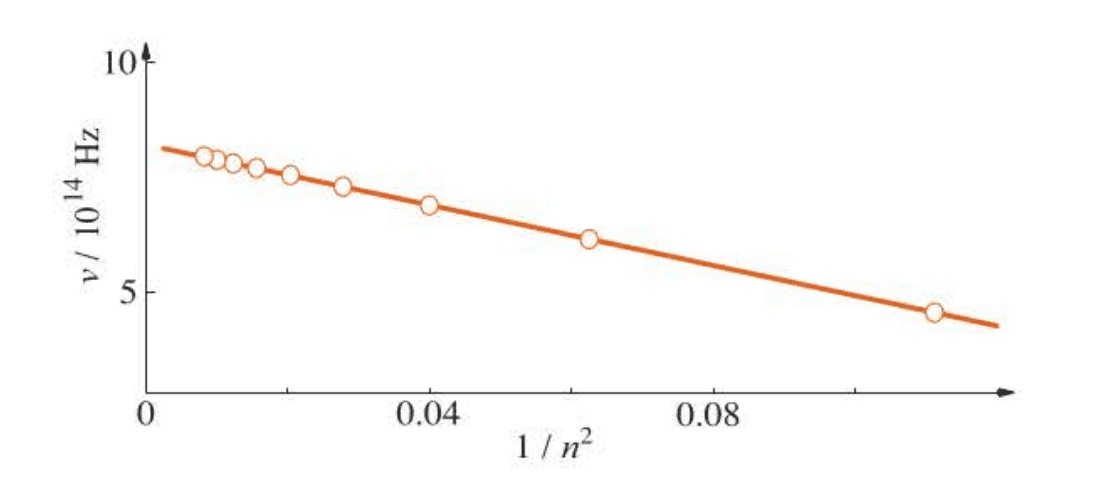
In particular, Balmer showed that the frequencies of the emission lines in the visible region of the spectrum could be described by the equation:

$\widetilde\nu = \frac \nu c=\frac 1 \lambda=109680 \left(\frac 1{2^2}-\frac 1{n^2} \right)cm^{-1} \quad n=3,4,\cdots$

This equation is called Balmer’s formula.

（ 巴尔末作为一个中学教师，能只依靠氢原子光谱的几条谱线猜出公式，并且与实验结果符合的如此之好，也确实是“如有神助”。 ）

Note that Balmer’s formula predicts a series oflines asn takes on the values 3, 4, 5, … This series of lines, the ones occurring in the visible and near ultraviolet regions of the hydrogen atomic spectrum and predicted by Balmer’s formula, is called the Balmer series. The Balmer series is shown in Figure 1.5.

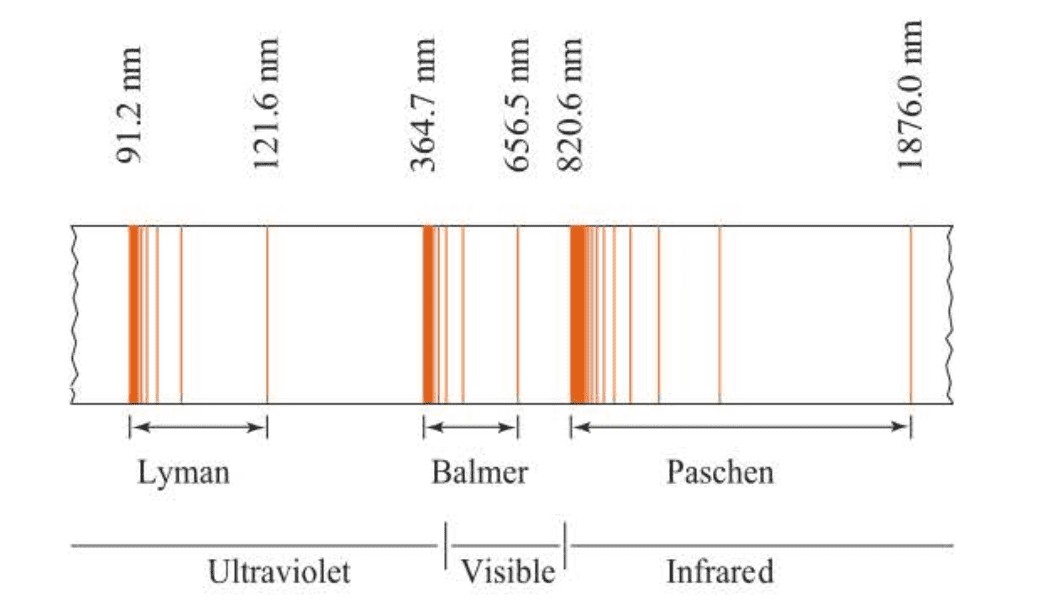
The Balmer series occurs in the visible and near ultraviolet regions. The hydrogen atomic spectrum has lines in other regions; in fact, series of lines similar to the Balmer series appear in the ultraviolet and infrared regions.

1.6 The Rydberg Formula Accounts for All the Lines in the Hydrogen Atomic Spectrum

The Swiss spectroscopist Johannes Rydberg accounted for all the lines in the hydrogen atomic spectrum by generalizing the Balmer formula to:

$\widetilde\nu=\frac 1{\lambda}=109680 \left(\frac 1{n_1^2}-\frac 1{n_2^2} \right)cm^{-1} \quad (n_2>n_1)$

where both $n_1$ and $n_2$ are integers but $n_2$ is always greater than $n_1$. This equation is called the Rydberg formula. The constant in Equation is called the Rydberg constant and Equation is commonly written as:

$\widetilde\nu=R_H \left(\frac 1{n_1^2}-\frac 1{n_2^2} \right)$

The modern value of the Rydberg constant is $109677.57cm^{-1}$, one of the most accurately known physical constants.

The spectra of other atoms were also observed to consist of series of lines, and in the 1890s Rydberg found approximate empirical laws for many of them. The really
interesting feature is that all the observed lines could be expressed as the difference between terms such as those in Equation. This feature was known as the Ritz combination rule.

（ 里兹组合规则说明了光谱项与谱线的关系，同时暗示了光谱线对于原子结构的表示，不过在当时，这还是一条无法从理论上说明的经验定律。 ）

1.7 Angular Momentum Is a Fundamental Property of Rotating Systems

（ 这一节并没有讨论量子力学的部分，而是回顾了一下经典物理学中有关转动的知识，这部分可以用以下的表格概括。 ）

Linear motion	Angular motion
Mass($m$)	Moment of inertia($I$)
speed($v$)	Angular speed($\omega$)
Momentum($p$)	Angular momentum($l=I\omega$)
Kinetic energy($T=\frac {mv^2}2=\frac {p^2}{2m}$)	Rotational kinetic energy($T=\frac {I\omega^2}2=\frac {l^2}{2I}$)

1.8 Bohr Assumed That the Angular Momentum of the Electron in a Hydrogen Atom Is Quantized

Classical physics predicts that an electron revolving around a nucleus will lose energy and spiral into the nucleus, and so a stable orbit is classically forbidden. It was Bohr’s great contribution to make two nonclassical assumptions. The first of these was to assume the existence of stationary orbits, in denial of classical physics. He then specified these orbits by invoking a quantization condition, and in this case, he assumed that the angular momentum of the electron must be quantized according to:

$l=m_evr=n\hbar \quad (n=1,2,\cdots)$

Solving the equation, we obtain:

$r=\frac {4\pi\epsilon_0\hbar^2n^2}{m_ee^2} \quad (n=1,2,\cdots)$

Thus, we see thatthe radii of the allowed orbits, or Bohr orbits, are quantized. The orbit with the smallest radius is the orbit with $n=1$, $r=52.9pm=0.529\mathring A$. The radius of the first Bohr orbit is often denoted by $a_0$.

The total energy of the electron is equal to the sum of its kinetic energy and potential energy. The potential energy of an electron and a proton separated by a distance $r$ is:

$V(r)=-\frac {e^2}{4\pi\epsilon_0r}$

The negative sign here indicates that the proton and electron attract each other; their energy is less than it is when they are infinitely separated $(V(\infin)=0)$. The total energy of the electron in a hydrogen atom is:

$E= \frac 12m_ev^2-\frac {e^2}{4\pi\epsilon_0r} \\[3mm] E_n=-\frac {m_ee^4}{8\epsilon_0^2h^2n^2} \quad (n=1,2,\cdots)$

Note that $n=1$ in Equation corresponds to the state of lowest energy, called the ground-state energy. At ordinary temperatures, hydrogen atoms, as well as most other atoms and molecules, will be found almost exclusively in their ground electronic state. The states of higher energy are called excited slates and are generally unstable with respect to the ground state. An atom or molecule in an excited state will usually relax back to the ground state and give off the energy as electromagnetic radiation.

（ 波尔的量子化假设说明了电子从高能级回到低能级时释放的电磁波能量为量子化的，很自然地解释了原子光谱线为什么是分立的。 ）

1.9 The Electronic Mass Should Be Replaced by a Reduced Mass in the Bohr Theory

（ 如本节小标题所说，对于电子绕核运动的二体系统，把二者的质量合在一起考虑会更为方便，这个总体的质量就称为Reduced mass，或者说折合质量。

在引入折合质量后，Bohr的这一套理论就能够很好的在氢原子上应用了，不过很可惜，也只能用于氢原子（以及类氢体系）。因为多电子系统会有其他更复杂的相互作用，需要我们继续扩展理论。 ）

1.10 Louis de Broglie Postulated That Matter Has Wavelike Properties

Scientists have always had trouble describing the nature of light. In many experiments light shows a definite wavelike character, but in many others light seems to behave as a stream of photons. Because light appears wavelike in some instances and particle-like in others, this disparity is referred to as the wave-particle duality of light.

In 1924, a young French scientist, Louis de Broglie, reasoned that if light can display this wave-particle duality, then matter, which certainly appears particle-like, might also display wavelike properties under certain conditions. This proposal is rather strange at first, but it does suggest a nice symmetry in nature. Certainly, if light can be particle-like at times, why should matter not be wavelike at times?

De Broglie was able to put his idea into a quantitative scheme.

$\lambda=\frac hp$

1.11 The de Broglie Formula Gives an Alternative Rationalization of Bohr’s First Postulate

Not only has de Broglie’s hypothesis led to the practical application of electron microscopy, but it was also a key step in our understanding of atomic structure. It can be used to give a simple, physical argument for the quantized Bohr orbits. As the electron revolves around the proton, it has wavelength $\lambda$. associated with
it. This situation is shown in Figure 1.6. For the orbit to be stable, it is reasonable to assume that the wave must “match,” or be in phase, as the electron makes one complete revolution. Otherwise, there will be cancellation of some amplitude upon each revolution, and the wave will disappear.

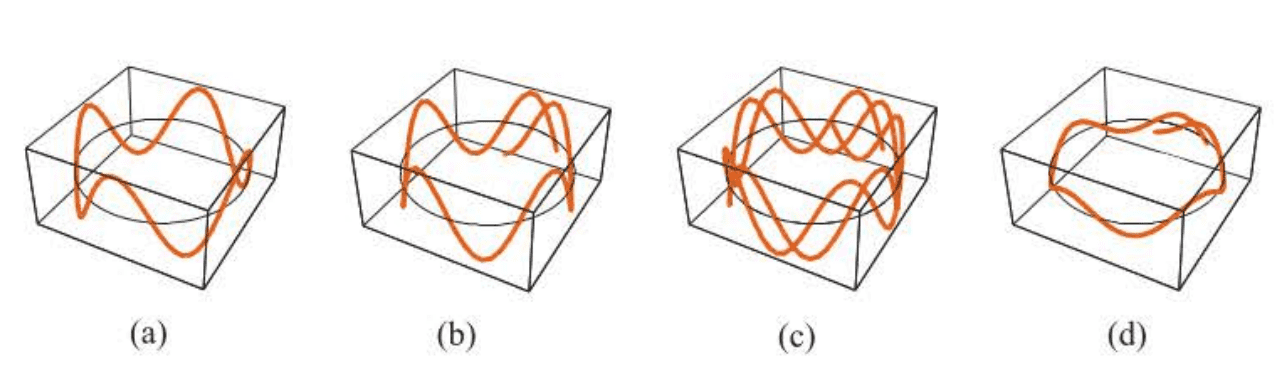
For the wave pattern around an orbit to be stable, we are led to the condition that an integral number of complete wavelengths must fit around the circumference of the orbit. Because the circumference of a circle is $2\pi r$, we have the quantum condition:

$2\pi r =n\lambda \quad n=1,2,3,\cdots$

If we substitute de Broglie’s relation into Equation, we obtain the Bohr quantization condition.

（ 之前我一直不太懂德布罗意波到底重要在哪里，为什么能被爱因斯坦誉为“揭开了巨大面罩的一角”。现在终于有所了解了，因为德布罗意物质波的提出，合理化了波尔的角动量量子化假设。在此之前，虽然波尔的理论可以应用，但是他给出的量子条件看起来莫名其妙，人们不能给出理论上的解释。物质波理论提出物质也具有波动性，那么就应当和光具有相同的表现，既然爱因斯坦已经指明了光量子化的合理性，那么波尔给出的量子条件就也理所应当了。 ）

1.12 De Broglie Waves Are Observed Experimentally

When a beam of X rays is directed at a crystalline substance, the beam is scattered in a definite manner characteristic of the atomic structure of the crystalline substance. This phenomenon is called X-ray diffraction and occurs because the interatomic spacings in the crystal are about the same as the wavelength of the X rays.

An interesting aside in the concept of the wave-particle duality of matter is that it was J. J. Thomson who first showed in 1895 that the electron was a subatomic particle and it was G. P. Thomson who was one of the first to show experimentally in 1926 that the electron could act as a wave.

1.13 Certain Two-Slit Experiments Exemplify Wave-Particle Duality

One of the principal experiments that displays the wave properties of light is the interference of two beams of light. The first experiment showing interference of light was performed by the British scientist Thomas Young around 1800.

it shouldn’t be surprising that a beam of electrons or any other atomic or subatomic particle will produce an interference pattern.

It is possible to perform a two-slit experiment such that only one particle at a time passes through the slits and to record its arrival at a second screen coated with a fluorescent film, which emits a brief burst of light at the point where it is struck. Using a suitable position-dependent recording device, we can record the arrival of each particle and accumulate the results. At low exposures, these tiny bursts of light appear more or less randomly over the film; but for longer exposures, hints of a pattern begin to emerge.

The three panels on the left record the arrival of 100, 300, and 3000 particles. The three panels on the right show the arrival of the same number of particles as those on the left, but one of the slits is closed, yielding no interference pattern.

Let’s now uncover both slits and try to detect which slit the particle passes through by setting up some sort of a detector behind one of the slits so that it can detect any particle that passes through that slit before it impinges on the fluorescent screen. We now know which slit the particle passes through on its way to the screen and don’t have to assume that it somehow passes through both slits simultaneously. We may know which slit the particle has gone through, but when we look at the fluorescent screen, we see that there is no interference pattern! The pattern is simply the one that would be obtained if one or the other slit had been covered. If we now turn off the detector, we obtain the interference pattern. It’s as if each particle behaves as a wave as it confronts the slits, unless we try to observe it, in which case it behaves as a particle.

We shall see that quantum mechanics is able to describe these experiments to great precision, in the sense of being able to predict the positions and the widths of the interference ridges. The physical interpretation of the results, however, is quite another matter.

1.14 The Heisenberg Uncertainty Principle States That the Position and the Momentum of a Particle Cannot Be Specified Simultaneously with Unlimited Precision

We now know that we must consider light and matter as having the characteristics of both waves and particles. Let’s consider a measurement of the position of an electron. If we wish to locate the electron within a distance $\Delta x$, then we must use a measuring device that has a spatial resolution less than $\Delta x$.

One way to achieve this resolution is to use light with a wavelength on the order of $\lambda \approx \Delta x$. For the electron to be “seen,” a photon must interact or collide in some way wiilh the electron, for otherwise the photon will just pass right by and the electron will appear transparent. The photon has a momentum $p=h/\lambda$, and during the collision, some of this momentum will be transferred to the electron. The very act of locating the electron leads to a change in its momentum.

If we wish to locate the electron more accurately, we must use light with a smaller wavelength. Consequently, the photons in the light beam will have greater momentum because of the relation $p=h/\lambda$. Because some of the photon’s momentum must be transferred to the electron in the process of locating it, the momentum change of the electron becomes greater.

（ 也就是说我们在测量过程中不可避免的会将光子的动量传递给电子，而且测量精度越高，所传递的动量也越多。 ）

German physicist Werner Heisenberg showed that it is not possible to determine exactly how much momentum is transferred to the electron. This difficulty
means that if we wish to locate an electron to within a region $\Delta x$, there will be an uncertainty in the momentum of the electron. Heisenberg was able to show that if $\Delta p$ is the uncertainty in the momentum of the electron, then

$\Delta x\Delta p \ge h$

The equation is called Heisenberg’s uncertainty principle and is a fundamental principle of nature. The uncertainty principle states that if we wish to locate any particle to within a distance $\Delta x$. then we automatically introduce an uncertainty in the momentum of the particle.

（ 这种不确定性的引入不是因为实验手段的缺陷或者实验仪器精度不足，它是测量这种行为本身的性质。同时也不难看出，不确定性原理（或者叫测不准原理）在宏观世界中几乎可以忽略，但是在微观尺度下就不得不考虑。 ）

总结

每本量子力学/量子化学/结构化学等书，第一章一般都是量子力学的发展史，了解这些内容有助于串起量子力学的整个发展历程，同时也能对关键发现的重要性有基本的掌握。

看了一章之后，我发现这本书的语言还是比较简单易读的，也许这会是一个好的预兆XD。